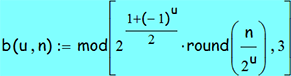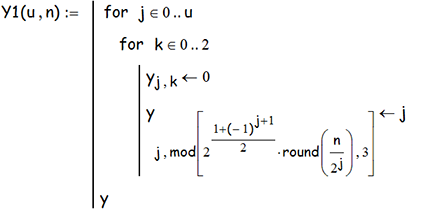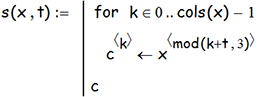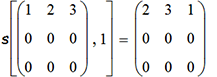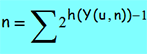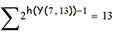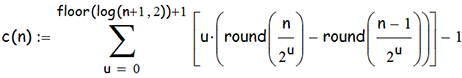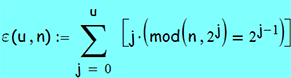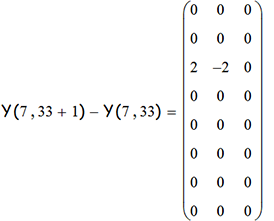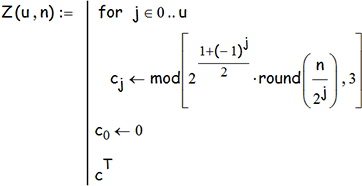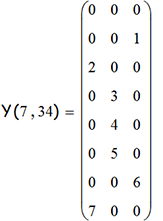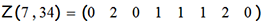Странное название, не так ли? По этому поводу есть старая пословица, которая в приличном варианте звучит примерно так: "Ну зачем козе баян?" Но на самом деле все слова и понятия, используемые в этом названии, существенно связаны между собой. Эти связи заслуживают пристального внимания и рассматриваются нами в данной статье.
Примечание 1: В математических расчётах я использую программу Mathcad 15. Интерфейс этой программы достаточно близок к общеупотребительному математическому языку. Я стараюсь разъяснить случаи возможного недопонимания. Кроме того, вся математика этой статьи может быть реализована и в других пакетах, например, в Excel.
Примечание 2: Эта статья не содержит больших математических открытий. Я лишь постарался обратить внимание на некоторые общеизвестные факты.
Статьи, в которых (как мне кажется) я сказал нечто новое, находятся в https://doi.org/doi:10.30970/ms.63.1.14-20
и в arXiv по адресу: https://arxiv.org/a/zhuravlov_v_1

Введение: Парадокс Рассела и Большой Взрыв

    Однажды я опубликовал следующий текст:
    "Вот вы говорите: рекурсия... Вы, разумеется, можете возразить, что ничего подобного никто из вас и не говорил. Ну, а если бы всё-таки говорили,- что бы я мог вам ответить? Наверное, вот что.
    Всё возможное всегда случается, ежели достаточно долго подождать. Вселенная устроена так, будто возникла она в некий момент прошлого. И согласно соотношению неопределённости между энергией и временем,- неточность фиксации этого начального момента порождает неточность нулевой энергии довселенского вакуума. Поэтому сработал туннельный переход из состояния с виртуальной ненулевой энергией в состояние с энергией реальной - случился Большой Взрыв, и Вселенная возникла... А если короче, то барон Мюнхгаузен вытащил себя из болота за собственные волосы! Вот и вся рекурсия - принципиально противоречивая основа всего бесконечного и всякой строгой, безупречно непротиворечивой логики. Именно такой процесс взаимоопределения реальности и понятия и был описан Гегелем в туманной философии, а затем обнаружен в самой точной математике...

     Так вот оно, оказывается, в чём дело! А вы говорите - рекурсия, рекурсия...
    Правда и то, что рекурсия никуда не исчезнет, даже если мы с вами, не только говорить, но и думать о ней забудем... А можем ли мы не думать о себе?"
     И сразу же я получил возражение: "туннельный переход не является рекурсией". Это возражение абсолютно справедливо и... является чисто формальным. Т.е. - истинное по форме, оно неверно в сущности.
    Когда происходит туннельный переход из состояния с "нулевой" реальной энергией (и "бесконечным" диапазоном виртуальных энергий), мы обнаруживаем, что реальное состояние в настоящий момент времени определяет состояния в прошлом. В итоге, имеем процесс, определяющий сам себя. И в этом состоит сущность вышеупомянутой гипотезы Большого Взрыва.
     Но в том и заключается смысл математической индукции и рекурсии - объект само-определяется (на этот раз не в физическом мире, а в арифметике,- натуральной или даже ординальной). И в этом состоит сущность рекурсивного процесса.
    Самоопределение выглядит красиво и парадоксально. Однако, сия парадоксальность чревата противоречием! Обратим внимание на известный парадокс Рассела, показавший невозможность "наивной" (не очень строгой, не достаточно формализованной) теории множеств Кантора. "Является ли своим элементом множество всех множеств, не являющихся своими элементами?" Вопрос неразрешим: каждый ответ влечёт своё отрицание. Избегают этого парадокса, лишь ограничивая, урезая и уточняя понятие множества. В одном из вариантов каждое множество считается элементом некого универсального множества - сильно ограниченного аналога интуитивного понятия "множества всех множеств". В другом варианте (в теории типов) произвольные совокупности элементов называются классами; множествами названы классы, которые являются элементами других классов. Сами же классы обладают лишь элементарными (алгебраическими) свойствами множеств. Есть и другие варианты. В любом случае речь идёт о таких формальных ограничениях понятия множества, которые исключали бы ситуацию, приводящую к парадоксу Рассела. Одним из вариантов мне представляется рассмотрение теории множеств в позитивной логике (в которой нет отрицания; ибо неконструктивное отрицание приводит к понятиям чрезмерно большого объёма противоречие в позитивной логике означает возможность доказать любое утверждение). Возможно также и построение теории множеств в квантовой логике, в которой возможны запутанные состояния утверждения и его отрицания...
    Впрочем, согласно теореме Гёделя о неполноте, теория множеств неполна принципиально. Поэтому, противоречие может возникнуть необязательно по причине возникновения парадокса Рассела. Опасность противоречий может появляться при рассмотрении "достаточно больших" бесконечных множеств. Но эти вопросы выходят за рамки нашей статьи. Вернёмся к нашим... козам.

Задача о волке, козе и капусте

    Нам надо переправить живой груз через реку. Груз - это волк, коза и кочан капусты. Волк может съесть козу, а коза может съесть капусту. Когда мы находимся рядом,- ситуация под контролем и никто никого не ест. Для переправы мы используем маленькую лодку, в которой можно поместить лишь один из этих объектов. Как переправить всех троих без потерь?
    Пока мы переправляем волка, коза съест капусту; пока мы переправляем капусту, волк съест козу. Мы можем спокойно переправить козу. Но потом, если поплывём за одним из оставшихся, а после - за другим, то либо волк съест козу, либо коза съест капусту,- в наше отсутствие. Так что же нам делать?
    Решение мы увидим, если обратим внимание на взаимоотношения всех трёх объектов. Итак: волк ест козу, коза ест капусту, но волк и капуста взаимно нейтральны. Центральное положение занимает коза: она может и съесть, и быть съеденной. В цепи из трёх звеньев центральное звено является единственным, имеющим два зацепления с соседями; оба других звена имеют лишь по одному зацеплению. Решение в том, что козу придётся перемещать дважды. Мы её перевозим, благополучно оставляя на берегу волка и капусту. Затем возвращаемся за капустой (или за волком), и перевозим козу обратно, оставляя капусту (или волка) на противоположном берегу; а потом перевозим волка (или капусту), оставляя на берегу козу; и только потом перевозим козу на берег, где нас благополучно дожидаются волк и капуста.
    Обратим внимание: решение заключается в повторяющихся действиях, которые иногда возвращают некоторые объекты к прежнему состоянию. Задачу можно попытаться обобщить, увеличивая длину цепи. Правда, тогда промежуточных звеньев будет больше одного - стоит нам отплыть на лодке, и они начнут "пожирать" друг друга. Есть ли у задачи обобщения? Есть! Но тогда ситуация усложнится.

Ханойская башня

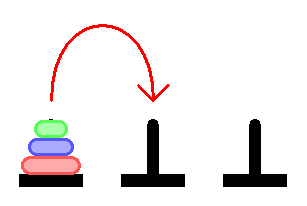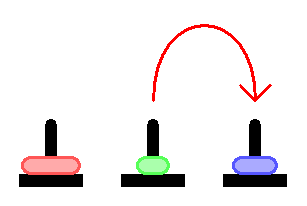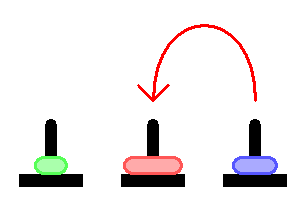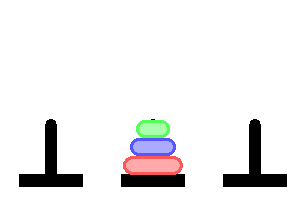
    Имеется три стержня. На первом нанизаны n дисков, упорядоченных по строго возрастающему диаметру; два других стержня пусты. На каждом ходу мы должны перемещать какой-нибудь диск с одного стержня на другой. Условие чисто физическое: мы можем переместить только верхний диск, лежащий на произвольном стержне. Второе условие: нельзя больший диск ложить на меньший. Наша цель - переместить все диски на один из пары пустых стержней.
    Процесс идёт примерно так:

 
    Приведу также статью, дающую формулировку задачи и её алгоритмические решения,- итеративное и рекурсивное (статья изложена практически полностью; к сожалению, написана она достаточно давно: в настоящий момент информация об авторе мною утеряна):

____________________________________________________________________________________________________

Ханойские башни

Автор:Быстрицкий В.Д.>
При написании статьи использовались материалы книги Ж. Арсака "Программирование игр и головоломок".

Головоломка "Ханойские башни" достаточно старая и хорошо известная, с ней связано несколько забавных легенд, но суть проблемы, которую я попытаюсь рассмотреть на примере данной задачи - использование рекурсивных алгоритмов и преобразование их к не рекурсивным.
Для начала сформулируем саму задачу. Даны три стержня ((н) - начальный, (к)- конечный, (д) - дополнительный) на стержень (н) нанизано некоторое количество дисков (будем полагать его равным n) при этом все диски имеют разный диаметр и расположены на стержне (н) в порядке уменьшения диаметра снизу в верх (см. рис).

 
Необходимо переместить все диски на стержень (к), т.е. головоломка должна быть приведена к виду:

 
при этом за один ход можно переместить только один диск, и в результате хода не должно возникнуть ситуации, когда диск с большим диаметром будет положен на диск с меньшим диаметром.

 
Выбор той или иной стратегии перемещения дисков приводит к новому вопросу, сколько необходимо ходов для того чтобы головоломка была полностью разрешена. Причем очевидно что количество ходов растет с ростом числа дисков, и желательно получить некоторую функцию f(n), которая выдавала бы для данной стратегии количество ходов необходимых для решения задачи в зависимости от числа дисков. В статье рассматривается только одна стратегия, оптимальность которой можно доказать. Вначале стратегия получается в виде рекурсивного алгоритма, а затем преобразуется к не рекурсивной форме.

Рекурсивная стратегия

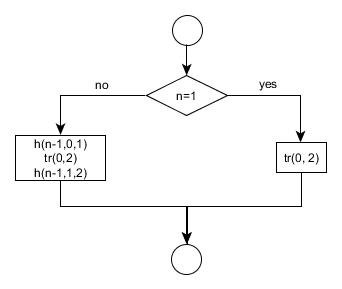
Итак, нам необходимо перенести n дисков со стержня (н) на стержень (к). Допустим у нас есть процедура перенесения n-1 диска, обозначим ее Х(n-1,(Ст1),(Ст2)), тогда задача легко разрешима для этого вначале перенесем n-1 диск со стержня (н) на стержень (д), применяя процедуру Х, затем перенесем n-ый диск со стержня (н) на стержень (к) (обозначим эту процедуру П((Ст1),(Ст2)) и наконец перенесем n-1 диск со стержня (д) на стержень (к). Работа выполнена. Алгоритм в этом случае можно записать следующим образом: 1. Х(n-1, (н), (д)) 2. П((н),(к)) 3. Х(n-1, (д), (к))

Теперь необходим частный случай, не являющийся рекурсивным. Если диск всего один, то можно сразу перенести его со стержня (н) на стержень (к), таким образом, выполняется тождество Х(1, (Ст1), (Ст2))=П((Ст1), (Ст2)). Таким образом, процедура Х представляется в виде блок-схемы:

 
Просто? Да, несомненно, просто, но все равно некоторым такое решение внушает опасение. Почему? Скорее всего, сказывается недостаток владения рекурсивными методами, но не только. Рекурсивные решения отличаются от обычных именно своей не очевидностью. Что же сделать, чтобы "поверить" в то, что предъявленная стратегия верна? На мой взгляд, лучший способ проверить стратегию "практически" для малых n. Вернемся к вопросу вычисления функции f(n). Для предъявленной рекурсивной процедуры, представление f(n) достаточно тривиально:
f(1)=1
f(n)=2* f(n-1)+1
Явный вид функции f(n) нетрудно найти из приведенных выше соотношений, пользуясь принципом математической индукции: f(n)=2ⁿ-1.

Дополнительно к тому, что уже имеется, заметим еще одно свойство перемещаемых дисков. Пусть наши диски пронумерованы от 1 до n, таким образом, что диск с наименьшим диаметром имеет номер 1, второй по величине диаметра диск номер 2, и т.д., наконец диск с наибольшим диаметром имеет номер n. Тогда можно заметить, два диска с номерами одинаковой четности никогда не будут лежать друг на друге (т.е. диск с номером 2 не ляжет на диск с номером 4, 6 или 8). Докажем что это свойство выполнено. Доказательство будем проводить по индукции, допустим, что свойство выполнено для процедуры Х(p,(Ст1),(Ст2)), где p < n (для p=1 и Х(1,(Ст1),(Ст2)) свойство выполнено автоматически), далее докажем, что тогда свойство выполняется и для Х(n,(Ст1),(Ст2)). Начнем с переноса (n-1) дисков на стержень (д). Пока не передвинут (n-1)-ый диск, ни один диск не кладется непосредственно на диск с номером n и значит требуемое свойство выполнено. Рассмотрим момент, когда n-2 дисков находятся на одном стержне, диски с номерами n-1 и n - на другом стержне, а третий стержень пуст. Мы перемещаем диск с номером n-1. Теперь нужно переместить первые n-2 дисков на диск с номером n-1, поэтому диски будут оказываться на диске с номером n. Если мы помещаем диск с номером k на диск с номером n, то для того, чтобы образовать пирамиду дисков с номерами от k до 1 и иметь возможность, переместить диск с номером k+1 на диск с номером n-1. Но поскольку требуемое свойство выполняется для n-1 дисков, то честность k+1 диска не может совпадать с четностью n-1. А значит, она совпадает с четностью n, и отсюда следует, что четность n и k различна.

Те из Вас кто склонен к пунктуальному разбору доказательств, может усмотреть некоторую нечеткость, но смею заверить, это не приводит к тому, что доказательство становиться "не законным", и сделано просто для сокращения изложения.

Итеративная стратегия

Итеративная стратегия основывается на рекурсивной, но при этом из решения полностью исключается рекурсия. Это хорошо с точки зрения практического понимания алгоритма (теперь его можно "пощупать").

Это не рекурсивный алгоритм "переброски" Ханойской башни. Вот он, метод (не знаю, описан ли он где-то: (литературы на эту тему я не встречал):
1. Порядок оптимального перемещения дисков однозначен и имеет вид (нумерация дисков ведётся с 1 - самый маленький, нумерация шагов - с 1):

Это не рекурсивный алгоритм "переброски" Ханойской башни. Вот он, метод (не знаю, описан ли он где-то: (литературы на эту тему я не встречал): 1. Порядок оптимального перемещения дисков однозначен и имеет вид (нумерация дисков ведётся с 1 - самый маленький, нумерация шагов - с 1): Шаг: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 ... Перемещаемый диск: 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 ... Нетрудно заметить (если хорошо присмотреться :)), что числа в нижней строчке показывают увеличенное на единицу количество делений без остатка, соответствующих верхних чисел на 2. 2. При оптимальном перемещении дисков каждый диск бывает последовательно на одних и тех же стержнях: Чётные диски: (н) (к) (д) (в цикле), нечётные диски: (н) (д) (к) (в цикле) или наоборот - в зависимости от количества дисков и целевого стержня. Для "переброски" необходимо запоминать текущее положение каждого диска. Далее - просто: определяем, какой диск, откуда, куда "кидаем", и, собственно, "кидаем"...

В верхней строке - нумерация шагов; в нижней - нумерация премещаемых дисков. Нетрудно заметить (если хорошо присмотреться :)), что числа в нижней строчке показывают увеличенное на единицу количество делений без остатка, соответствующих верхних чисел на 2.
2. При оптимальном перемещении дисков каждый диск бывает последовательно на одних и тех же стержнях: Чётные диски: (н) (к) (д) (в цикле), нечётные диски: (н) (д) (к) (в цикле) или наоборот - в зависимости от количества дисков и целевого стержня. Для "переброски" необходимо запоминать текущее положение каждого диска. Далее - просто: определяем, какой диск, откуда, куда "кидаем", и, собственно, "кидаем"...
На самом деле этот алгоритм переброски, если хорошо присмотреться, получается из рекурсивного. Поэтому избавимся от рекурсии и докажем, более или менее строго, некоторые факты. Заметим вначале, что, в силу условий налагаемых на перемещение дисков, всегда диск с номером 1 находится на вершине одного из стержней. И на любом шаге мы можем переместить либо диск 1, либо один из дисков (с наименьшим диаметром) находящихся на вершине стержня отличного от того на котором расположен диск с номером 1. Из всего этого можно сделать вывод, что диск один перемещается один раз в каждые два хода, иначе расположение дисков повторялось бы. Покажем, что наш первый диск всегда перемещается по одной из выбранных стратегий: либо (н)-(д)-(к), либо (н)-(к)-(д), причем выбор той или иной стратегии зависит от четности общего количества дисков n. Доказательство проведем индукцией по общему числу дисков n. Допустим, что в процедуре Х(n-1,(н),(к)) диск 1 перемещается всегда в одном направлении. Тогда для Х(n,(н),(к)) нам необходимо выполнить Х(n-1,(н),(д)) и Х(n-1,(д),(к)), т.е. вместо того чтобы непосредственно переходить от стержня (н) к стержню (к) мы делаем этот переход, используя стержень (д) , другими словами мы делаем два перехода в обратном направлении. При этом диск 1 продолжает перемещаться всегда в одном и том же направлении, но это перемещение меняется при переходе от n-1 к n. Поскольку при n=1 диск 1 перемещается с диска (н) на диск (д), то такое перемещение сохраняется для всех нечетных n. В то время как для четных n он будет перемещаться согласно стратегии (н)-(д)-(к).
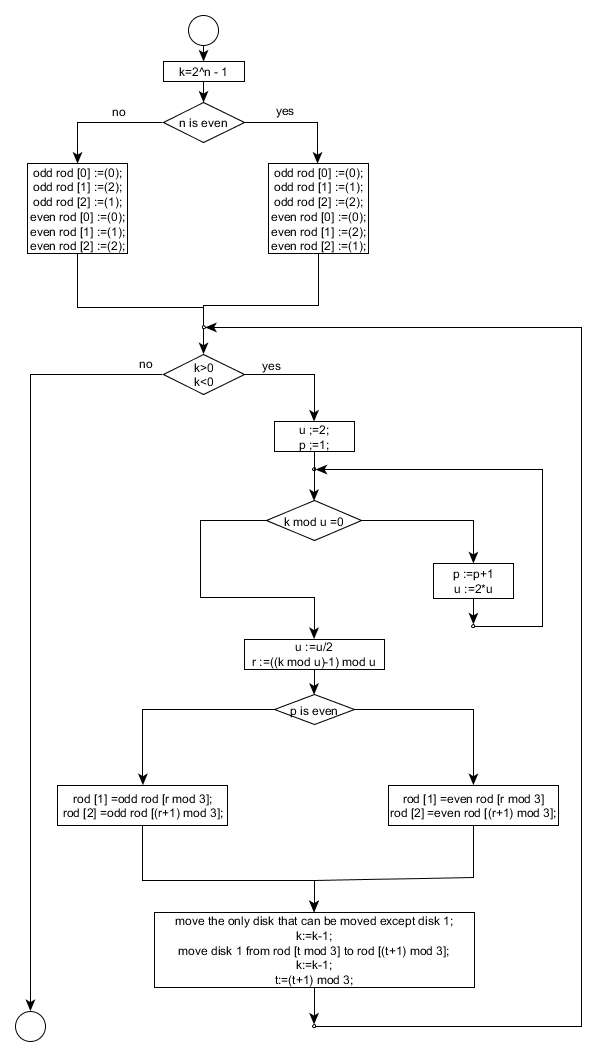
В принципе уже это дает нам возможность представить итеративный алгоритм перемещения дисков, который имеет вид:

 
Неплохой алгоритм, если мы хотим перемещать диски вручную, но фраза "переместить единственный диск, который можно переместить, кроме диска 1" выглядит недостаточно конкретно.
Номер любого хода можно единственным образом представить в виде k=(2r+1)2^p-1.
Итак, первое, что нам надо доказать, это то, что на шаге с номером k мы перемещаем диск, номер p. Для p=1 это тривиально, он действительно перемещается каждый нечетный ход. Возвращаясь к рекурсивному алгоритму, заметим, что перенос диска с номером p, происходит только внутри процедуры Х(p,(Ст1), (Ст2)), а между двумя вызовами этой процедуры, происходит одно перемещение диска (алгоритм Х - П - Х), причем число шагов необходимых для выполнения процедуры Х(p,(Ст1), (Ст2)) равно значению функции f(p). Таким образом, первое перемещение p-го диска происходит на шаге f(p-1)+1=2^p-1, а каждое следующие через 2^p-1-1+1+2^p-1=2^p-1 шагов, т.е. номера шагов, когда мы перемещаем p -ый диск действительно имеют вид k=(2r+1)2^p-1k=(2r+1)2^p-1. При этом, как мы показали, диски с нечетными номерами перемещаются по той же стратегии, что и диск номер 1, диски с четными номерами по обратной стратегии. Таким образом, теперь мы можем конкретизировать приведенный выше итеративный алгоритм:

 
Я надеюсь, что данная статья еще раз подчеркнула, тот факт, что при помощи рекурсии многие задачи решаются легко и красиво, что называется "в две строки". Решение той же проблемы, без использования рекурсии, приводит к серьезным сложностям, даже тогда когда мы уже имея рекурсивный алгоритм, пытаемся его просто переработать.
____________________________________________________________________________________________________

Формульные решения: вычисление состояния башни в произвольный момент времени.

    Помимо "неочевидности (неявности?)", есть ещё один изъян рекурсивных решений: они занимают много времени. Задача ханойской башни похожа на известную легенду, в которой царь попросил изобретателя шахмат назвать желаемую награду. Изобретатель попросил сущий пустяк: за первую клетку шахматной доски 1 зёрнышко пшеницы, а за каждую последующую - в 2 раза больше. Задача оказалась неразрешимой технически и материально. Так и с башней: требуется (2^u - 1) шагов для переноса u дисков на другой стержень,- со всеми вытекающими последствиями. Утешительно то, что дело облегчается, если найти нерекурсивное решение в виде явной формулы, вычисляющей состояние башни по числу шагов, необходимых для её построения - тогда не требуется вычислять башню на всех предыдущих шагах. Более того, можно избавиться не только от рекурсии, но и от итераций. Вот она, эта формула:


Это столбец диска u на n-ном ходу; т.е. - башня представляется в виде матрицы (индексация строк и столбцов начинается с 0 (просто ради некоторого удобства вычислений); таким образом, верхняя строка матрицы всегда равна 0, а диски, всегда вполне упорядоченные по возрастанию их диаметра, начинаются с 1-го и кончаются u-тым); round( ) и mod( ,3) - обычные функции округления и взятия по модулю 3.
    Это простая арифметическая формула, которая воплощает через элементарные функции те же идеи, что известный алгоритм Грея, основанный на подсчёте числа бит, необходимых для перемещения каждого диска.
    Алгоритмически: формула утверждает, что:

1) На каждом ходу двигается только тот диск, который не двигался на предыдущем.
2) Все диски движутся циклически (по модулю 3); причём, чётные диски перескакивают вправо через стержень, а нечётные - переходят вправо на соседний (при этом "чёт и нечет", а также "вправо и влево" можно поменять местами одновременно для всех дисков).

    Но ценность формулы в том, что она не рекурсивна и не итеративна: мы можем просто вычислить состояние башни для любого номера хода, не проходя её предыстории.
    Эту формулу, как и все последующие, я привожу без доказательств (но даю примеры их работы) потому, что они легко доказываются по индукции,- что характерно для рекурсивных процессов; эти формулы я вывел сам и нигде их не встречал. Однако, думаю, что речь идёт об известных в математике фактах.
    В противоположном направлении всё пойдёт, если в степени 2-ки u+1 заменить на u. Это и будет алгоритм обратного перехода (когда из данного состояния башни, считая число шагов до восстановления её начального состояния, мы получаем число шагов до получения данного состояния. Но путь итеративный. Который, как мы уже отмечали, чрезмерно удлиняется при увеличении числа дисков u. Можно и по прямой формуле прийти в исходное состояние, считая шаги (фактически, это тоже итеративный путь).
    Исходя из этой формулы, легко строится программа, выдающая матрицу башни u на n-ном ходу:

 

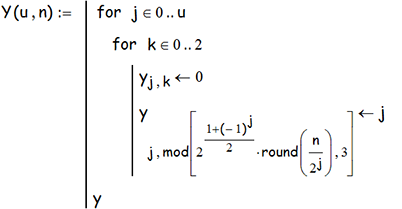
Вариант Y использует перемещение дисков слева направо; вариант Y1 - наоборот. Иллюстрацией формулы и работы программы служит фильм, показывающий перемещение на другой стержень башни из 7-ми дисков:

number.avi.

     После просмотра фильма мы видим, что:

1) Диски всегда вполне упорядочены по диаметру, чего и требуют условия задачи.
2) Чётные и нечётные номера дисков всегда чередуются, о чём уже говорил Быстрицкий в своей статье.
3) Будучи нерекурсивной, наша формула работает всегда (а не только на 7-и дисках), так как перемещение башни всегда рекурсивно: чтобы построить бОльшую башню, надо дважды построить меньшую, как отмечал Быстрицкий.
4) Формула подтверждает: для перемещения башни из n дисков надо сделать 2^n-1 шагов (127 при n=7). Отличие формулы от конструктивного (рекурсивного) алгоритма в том, что она позволяет найти конфигурацию башни очень быстро, даже для очень больших n. Алгоритм же может привести нас к удручающей, (по времени) ситуации: задача может оказаться невыполнимой практически. Однако же, возможны ситуации, когда практическое выполнение задачи может быть только рекурсивным... Это не только конфликт между конструктивной математикой и формальной. Это несоответствие между мышлением и реальностью, которое настолько же загадочно, как и соответствие между ними. Это основа вечных вопросов философии.

Обратная задача

     Как по состоянию башни узнать номер хода, при котором оно возникло? Для этого нам потребуется вспомогательная программка:

- это циклическая перестановка 3-х столбцов матрицы (моделирующих стержни, как мы уже говорили); например:


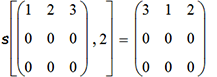
     Теперь по матрице Y(u,n) вычисляем номер хода n, на котором эта матрица возникла:



- это вектор степеней двойки для нижеследующей суммы:


которая и даёт нам искомый номер соответствующего хода; например:

     Механизм этой процедуры таков. Максимальный по величине диск u, сдвинутый с нулевого положения, даёт нам нижнюю оценку числа n; это 2^u-1 - ровно столько ходов надо для того, чтобы передвинуть башню (u-1) и сдвинуть диск u. И теперь надо вернуть "подбашню" в нулевое положение (вернуть, циклически сдвинув всю матрицу), после чего снова ищем максимальный диск, сдвинутый с нулевого положения, и т.д..
     Это тоже "возвратная" рекурсия. Однако, рекурсия по числу дисков, а не по числу ходов; получается гораздо меньше; и шаг рекурсии необязательно единичный (он переменный). Всё это сильно экономит время вычислений.

Чётность и системы счисления

        Эти оставшиеся темы не связаны прямо. И я не могу сказать о них много. Поэтому я объединил их одним заголовком.
     Замечание. Применяя наши формулы и программы, необходимо следить за граничными условиями. Например, состояние башни на n-м ходу можно вычислять для любого числа дисков u и при любом n. Однако при n>3*(2^u - 1) диски будут совершать (правильные!) циклические движения, бесконечно перемещая башню по 3-м стержням. И для обратной процедуры надо брать башни, в которых n меньше или равно (2^u - 1). В то же самое время, не нужно забывать, что u, число дисков башни, может быть потенциально бесконечным; а u-башня, первые (2^u - 1) ходов будет вести себя также, как и (u+1)-башня. Во избежание недоразумений, следует рассматривать только те случаи, когда n<2^u.
     Это функция чётности числа n, откалиброванная так, что на выходе имеем степень чётности числа n, (т.е. степень 2, в разложении n в произведение степеней простых сомножителей:


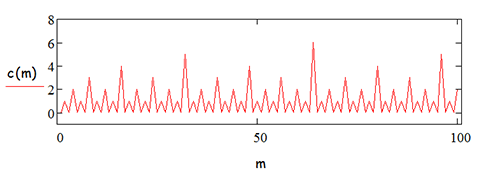
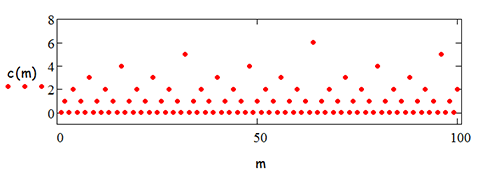
     Обратим внимание на её графики (первый в виде линии, второй - в виде точек):




     Все нечётные числа придают функции значение 0; как известно, нечётные числа составляют "половину" всех чисел. Числа, однократно делимые на 2 составят "четвёртую часть", и т.д., что и показывают графики (кавычки " " говорят о том, что наши утверждения "асимптотически" верны для всех конечных множеств m:={1,..., u} ).
     Но наблюдая за поведением башни, видим, что числа (равные диаметрам) её дисков ведут себя точно также: 1 совершает каждый нечётный ход, 2 - каждый единожды чётный, 3 - каждый 8-й ход, и т.д. Причём, каждое из этих чисел имеет свою фазу начала движений: 1 будет первой, а произвольный диск начнёт своё движение с 2^u-1-го хода. Отсюда делаем вывод, что ε(u, n)=c(n)+1 при достаточно большом u, где ε(u, n) определяется формулой:


- где равенство означает характеристическую функцию соответствующего множества.
     Т.е. - эта формула тоже является определением функции чётности (откалиброванной так, что ε(u, n)=с(n)+1). И она же показывает нам, какой диск сдвинется на n-ном ходу. Например: ε(7,34)=с(34)+1=2.
     А поскольку нам известно что все чётные диски совершают циклические перемещения последовательно, а нечётные - "через один столбец", и что бОльший диск не может накрыть меньший, то теперь мы имеем ещё один нерекурсивный и неитеративный алгоритм вычисления состояния башни. Проверить работу этих вычислений можно, взяв разницу матриц башни на соседних ходах:


Это значит, что на 34-м ходу двойка сдвинулась со 2-го диска на 0-ой, что мы и вычислили только что; если диск неподвижен, то его позиция обнуляется.
     Но обратимся к различным формам отображения башни как математического объекта. Вот программа, выдающая нам линейный список номеров столбцов u-башни на n-м ходу:


Например, вычисляем матрицу 7-башни на 33 и 34 ходах:

 

 
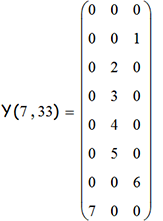
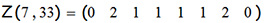
     Функция чётности весьма интересна. Будучи квазипериодической, для всякого u, она, начиная с момента 2^u-1, локально взаимно однозначна на периоде 2u. Это позволяет нам рассмотреть ханойскую башню как систему счисления. Возможно, такая система счисления окажется практически полезной.

Заключение

     В заключение мы покажем несколько иллюстраций описанных процессов. Глядя на графики, мы видим фрактальную природу башни: каждое следующее число продвигается с частотой, в 2 раза меньшей предыдущего. Нижеследующие орнаменты получены некими преобразованиями башни (сейчас я уже не помню, какими):

 
Это и не удивительно - фракталы имеют принципиально рекурсивную природу.
     Возможно, функцию чётности можно как-то связать с вейвлетом Хаара.
     А вот ещё интересные иллюстрации. Я подумал о том, что 3 стержня башни можно пустить по кругу, как аргумент в комплексном числе... В данном случае, мы изображаем диски точками, проходящими по такой окружности на постоянных уровнях и соединёнными отрезками прямых:

nunchaku.avi

- это всё та же 7-башня. Получается этакая нунчаку из 7-ми сегментов, которую вертит невидимый мастер, стоящий в центре окружности. Что, если сделать функцию чётности непрерывной (в данном случае, при помощи параболической интерполяции), превращая нунчаку в эффектную экзотическую плётку:

Zmyej.avi

     Думаю, тут есть много разных возможностей, в том числе и для практического применения. Но это уже выходит за рамки нашей работы.
     Похоже на то, что все конечные рекурсивные задачи можно решить и без рекурсии; и похоже, всякая бесконечность без рекурсии невозможна. И она (эта самая бесконечность) вплотную приближает нас к противоречию. Хотелось бы обратить внимание: рекурсия (индукция) есть первая (ещё примитивная) математическая модель авторефлексии, самоопределения объекта (по Гегелю), которая и создаёт "бытие для иного" из "бытия в себе и для себя". А ведь всё начинается достаточно просто: бесконечное множество равномощно своему собственному подмножеству.
     Что ж... На данном этапе мне остаётся лишь, со всем возможным смирением, созерцать Ханойскую башню и размышлять, размышлять...

Osyol.avi

Библиография

Эту пару книг легко найти в рунете:

[1] Haskell B. Curry, McGraw-Hill Book Company, INC.
Foundations of Manthematical logic, (1969).
Карри, Основания математической логики.

[2] By.G. Polya, Ptinceton University Press,
Patterns of plausible reasoning, (1954)
Джордж Пойа, Математика и правдоподобные рассуждения.