Уткин Владимир. Парадоксальный резонансный преобразователь напряжения

ПАРАДОКСАЛЬНЫЙ РЕЗОНАНСНЫЙ ПРЕОБРАЗОВАТЕЛЬ НАПРЯЖЕНИЯ

("чудеса" резонанса)

Владимир Уткин u.v@bk.ru

В статье рассматривается резонансный преобразователь напряжения на основе пары связанных резонансных контуров.

Парадокс данного резонансного преобразователя заключается в том, что для повышения напряжения в N раз, соотношение витков в контурах должно образовывать понижающий напряжение в N раз трансформатор. А для понижения напряжения в N раз, соотношение витков в контурах должно образовывать повышающий напряжение в N раз трансформатор. Структурная схема резонансного преобразователя приведена ниже на Рис.1.

0x01 graphic

Рис.1 Структурная схема резонансного преобразователя на основе пары связанных резонансных контуров при разном числе витков в контурах, где ї₂резонансная частота связанных контуров.

Кроме того, данный преобразователь может быть построен для случая, когда число витков в контурах совпадает. В этом случае выходное напряжение определяется соотношением ёмкостей конденсаторов, подключенных к первичному и вторичному контуру. Для повышения напряжения в N раз ёмкость конденсатора вторичного контура должна быть в N раз меньше ёмкости конденсатора первичного контура. Для понижения напряжения наоборот. Структурная схема такого варианта представлена ниже на Рис.2.

0x01 graphic

Рис.2 Структурная схема резонансного преобразователя на основе пары связанных резонансных контуров при равном числе витков в контурах, где ї₂резонансная частота связанных контуров.

Идея обоих вариантов преобразователя основана на теории связанных резонансных контуров. Эту теорию можно подробно изучить по учебнику, указанному в конце статьи. Либо в Интернете по запросу:" Связанные резонансные контуры".

Из теории известно, что при коэффициенте связи контуров К> 0.7 их резонансная кривая приобретает "двугорбый" вид с резонансами на частотах ї₁ и ї₂, показанный на Рис.3. Чем больше коэффициент связи контуров К, тем больше отличаются резонансные частоты ї₁ и ї₂, которые определяются по следующим формулам.

0x01 graphic

Происходит это за счёт того, что фаза колебаний во вторичном контуре на частоте ї₂ отличается на 180 градусов от фазы колебаний в первичном контуре. В результате электромагнитные поля катушек контуров направлены встречно и подавляют друг друга. Откуда следует, что чем ближе катушки друг к другу (больше коэффициент связи К), тем сильнее подавление и выше резонансная частота ї₂за счёт уменьшения эффективной индуктивности катушек.

0x01 graphic

Рис.3 Резонансные кривые связанных резонансных контуров в зависимости от коэффициента связи К.

При этом в литературе рассматривается вариант связанных резонансных контуров, когда они идентичны. То есть, совпадают индуктивности и ёмкости первого и второго контура.

В тоже время, резонансы будут наблюдаться, даже тогда, когда параметры первого и второго контура не совпадают. Правда на других частотах ї₁ и ї₂, но всё равно будут наблюдаться. И вот здесь происходит самое интересное с точки зрения преобразования напряжения. Напряжение на выходном контуре будет зависеть от резонансной частоты ї₂, определяемой соотношениями индуктивностей и ёмкостей связанных контуров. То есть, чем выше будет резонансная частота ї₂ в зависимости от указанных параметров, тем выше будет напряжение на выходном контуре. Обобщённые графики этой зависимости представлены на Рис.4 для случаев (А) и (В).

0x01 graphic

Рис.4. Зависимость резонансной частоты ї₂ и напряжения U₂ на выходном контуре от соотношения числа витков контуров - вид (А), и соотношения ёмкостей конденсаторов С₂/С₁ при равном числе витков контуров - вид (В).

Эти зависимости и лежат в основе структурных схем преобразователей, показанных на Рис.1 и Рис.2.

Принципиальные схемы простейших резонансных преобразователей напряжения, построенных на изложенном принципе показаны на Рис.5.

0x01 graphic

Рис.5. Простейшие схемы парадоксального резонансного повышающего преобразователя напряжения для случая разного числа витков в контурах - (А), и случая равного числа витков в контурах - (В).

По сути это обычные LC генераторы с трансформаторной обратной связью. Однако, чтобы заставить их работать на частоте ї₂ катушка положительной обратной связи L₃ включается в полярности противоположной "общепринятой", чтобы заставить резонансные катушки создавать встречные электромагнитные поля. И располагается эта катушка положительной обратной связи пространственно вместе с катушкой L₂.

При этом, катушки L₁ и L₂ должны иметь коэффициент связи K в пределах от 0,7 до 1, в соответствии с теорией. Но сама величина коэффициента связи К практически не влияет на величину преобразования напряжения (если нет потерь в индуктивностях и ёмкостях). А только меняет рабочую частоту схем. При коэффициенте связи К стремящемся к единице рабочая частота схем стремится к бесконечности.

Если все вышеуказанные условия не соблюдены, то схемы превращаются в обычные LC генераторы, работающие на частоте ї₁. И как следствие "чудо" не происходит.

В процессе экспериментов были апробированы оба варианта резонансного повышающего преобразователя. Однако, ниже приводятся результаты только для преобразователя с равным числом витков в контурах - вариант (В), с повышением напряжения в восемь раз.

Контура были изготовлены на основе тороидального сердечника 100х60х14 600НН (не принципиально) и содержали по 64 витка эмалированного провода, намотанных на противоположных сторонах магнитопровода (чтобы несколько снизить коэффициент связи катушек). Катушка связи L₃ содержала 16 витков провода и располагалась компактно поверх катушки L₂ точно в её центре.

В качестве транзистора использовался 2N2222A, резистор использовался номиналом 20 Ком. Ёмкости конденсаторов для увеличения напряжения в восемь раз отличались также в восемь раз С₁=0,2 мкф и С₂=0,025 мкф. Источник питания использовался напряжением 1,5 Вольта.

Результаты эксперимента в виде осциллограмм, наблюдавшихся на первичном и вторичном контуре представлены на Рис.6. В начале без повышения напряжения (оба конденсатора ёмкостью по 0,2 мкф) и с повышением напряжения (ёмкость выходного конденсатора 0,025 мкф). Там же показан внешний вид использовавшихся контуров. В качестве нагрузки использовались пять пар светодиодов на 3 Вольта (5213UWC, 20000 mCd, 3 -3,6V), соединённых встречно/параллельно, и показанных в правой части рисунка.

Красным показаны осциллограммы напряжения на входном контуре, жёлтым осциллограммы напряжения на выходном контуре.

0x01 graphic

Рис.6. Осциллограммы напряжений на входном и выходном контуре при равных величинах ёмкостей конденсаторов С₁ и С₂ и при отличии ёмкостей в восемь раз.

Как видно из представленных результатов, при уменьшении ёмкости выходного конденсатора в восемь раз с 0,2 мкф до 0,025 мкф амплитуда колебаний на выходном контуре также возросла в восемь раз. А частота колебаний повысилась с 22 кГц до 49 кГц. Подключённые светодиоды начали светиться, хотя и не очень ярко.

В заключении следует сказать, что поставленные эксперименты полностью подтвердили подход по созданию резонансного преобразователя напряжения на основе пары связанных резонансных контуров. При этом автор не ставил целью изучить КПД данного преобразователя, или оптимизировать режим генераторного транзистора. Целью являлось желание показать работоспособность данного подхода. Возможность объединения вариантов (А) и (В) является очевидной.

ЧАСТЬ 2

В этой части рассмотрим некоторые особенности работы парадоксального резонансного преобразователя напряжения для случая повышения напряжения.

Если посмотреть на параметры первоначальной настройки контуров при повышении напряжения, то можно заметить, что вторичный контур всегда изначально настраивается на более высокую резонансную частоту чем первичный контур (за счёт меньшего числа витков катушки или меньшей ёмкости конденсатора). При такой ситуации контура вступить в резонанс не могут. Следовательно, чтобы оба контура вступили в резонанс на частоте ї₂, частота первичного контура должна быть повышена до уровня частоты вторичного контура. Иначе резонанса не будет. Как это может произойти?

В преобразователе это происходит за счёт встречного электромагнитного поля от вторичной катушки, возникающего при частоте ї₂ и "сжимающего" поле первичной катушки, что приводит к уменьшению её эффективной индуктивности - Рис. 7 справа. В результате чего резонансные частоты контуров выравниваются.

0x01 graphic

Рис. 7 Поле вторичной катушки "сжимает" поле первичной катушки при резонансном повышении напряжения (справа). В отличие от случая когда повышения напряжения нет (слева).

Откуда следует, что для наступления резонанса при повышении напряжения, энергия вторичного контура должна быть всегда больше энергии первичного контура. В противном случае энергии не хватит чтобы "поджать" поле первичного контура, что необходимо для наступления резонанса. Таким образом, резонанс с повышением напряжения может возникнуть только тогда, когда энергия вторичного контура больше энергии первичного контура. При этом, нарушения закона сохранения энергии здесь нет, так как контура представляют собой единую связанную систему, в которую энергия поступает от внешнего источника.

Таково самое грубое объяснение происходящих процессов при резонансном повышении напряжения (без упоминания фазовых соотношений, хотя именно они приводят к требуемому результату).

Далее на практике постараемся проиллюстрировать приведённое простейшее объяснение. Перейдём к экспериментам. Повторим ранее проведённый эксперимент с повышением напряжения в восемь раз, добавив дополнительные измерительные катушки (по 32 витка) на магнитопровод и вне его. Местоположение этих измерительных катушек на магнитопроводе и вне его подберём так, чтобы при работе преобразователя генерируемая этими катушками ЭДС была равна нулю (чтобы определить места где встречные поля первичной и вторичной катушки равны). В результате получим то, что показано на Рис.8.

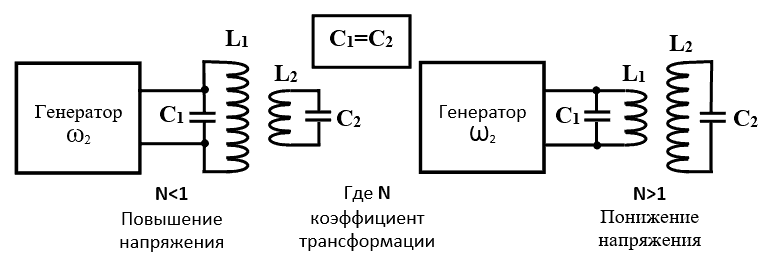
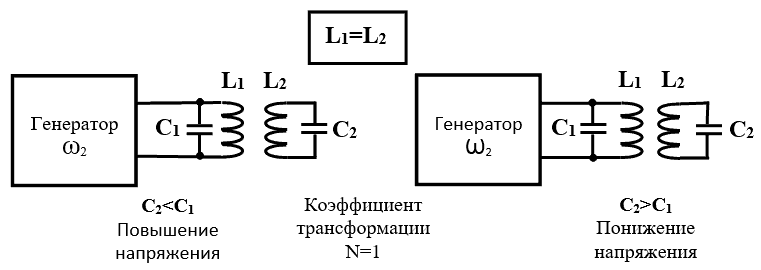
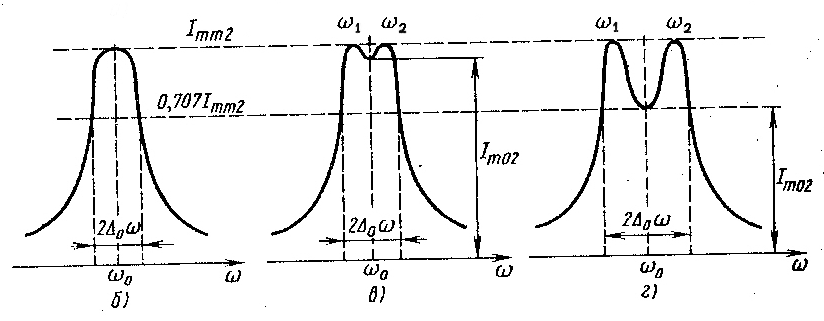
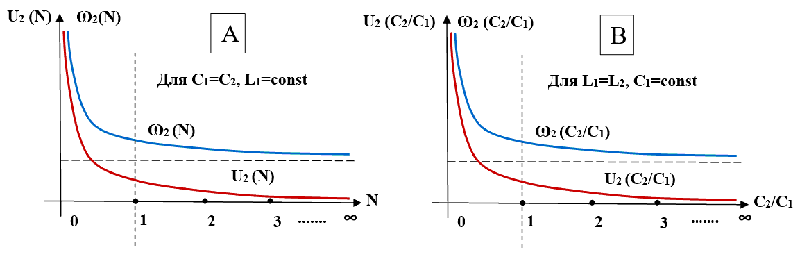
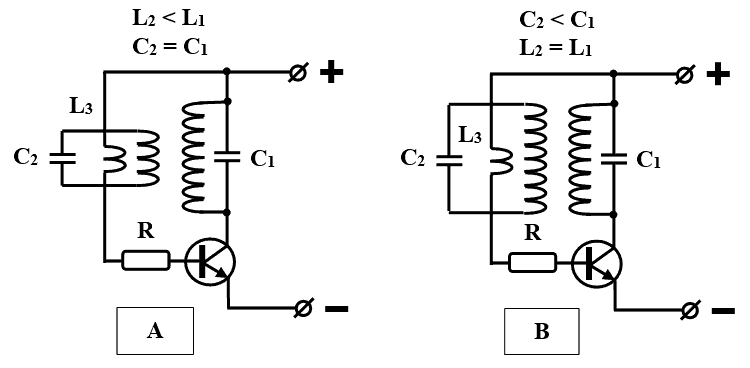
0x01 graphic

Рис. 8 Местоположение детектирующих катушек, выдающих нулевую ЭДС. Для случая без повышения напряжения (слева), и случая с повышением напряжения в восемь раз (справа).

Как видно из Рис.8, положение детектирующих катушек, размещённых на магнитопроводе, хорошо согласуется с ориентацией полей, показанных на Рис.7. Что экспериментально подтверждает "сжатие" поля первичной катушки полем вторичной катушки для выравнивания резонансных частот при повышении напряжения, иллюстрируя приведённое ранее объяснение.

Однако, можно заметить, что внешние детектирующие катушки выдают нулевую ЭДС при их неизменном положении. Что несколько неожиданно, и является ещё одним парадоксом данного преобразователя.

Такой результат наводит на мысль о том, что при подаче возбуждающего напряжения на детектирующие катушки, расположенные на магнитопроводе (вместо первичной катушки), на них не будет наблюдаться резонансное напряжение связанных контуров. То есть, если возбуждающее напряжение было в виде импульсов, оно таким и останется даже после возникновения гармонических колебаний резонанса.

Для подтверждения данного предположения был проведён соответствующий эксперимент с использованием внешнего генератора импульсов и детектирующих катушек в качестве катушек возбуждения. При этом, катушки включались последовательно и располагались как на Рис.8 справа. Результирующие осциллограммы приведены на Рис.9.

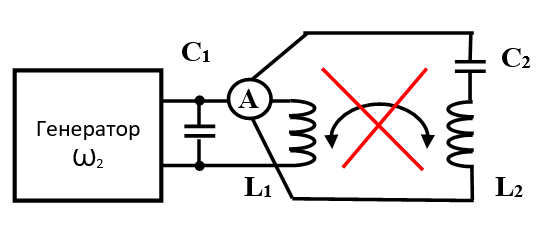
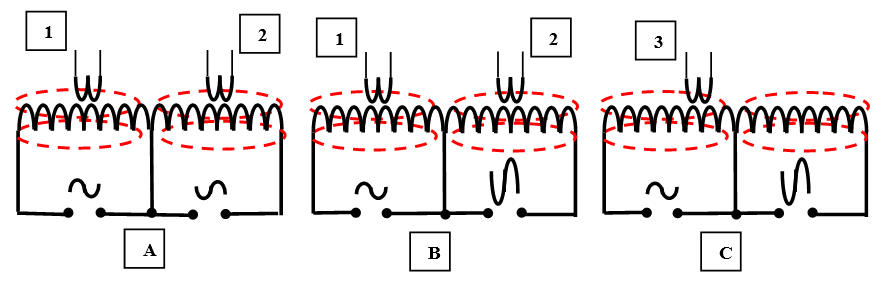
0x01 graphic

Рис. 9 Осциллограммы напряжений на возбуждающих катушках (красный) и резонансной вторичной катушке (жёлтый). Вне резонанса (54 кГц) - слева и при резонансе (48 кГц) - справа.

Как видно из Рис.9 форма напряжения на возбуждающих катушках не зависит от наличия резонанса. То есть, возбуждающие катушки "не видят" резонансных колебаний связанных контуров, если их поместить в места где суммарное резонансное поле равно нулю. Что подтверждает сделанное ранее предположение.

Кроме того, следствием "сжатия" поля первичной катушки также является специфическое распределение напряжения, возникающее вдоль её длины, показанное слева на Рис.10. Откуда следует, что напряжение на центральной части первичной катушки должно быть больше чем напряжение на всей катушке. Что легко можно проверить разместив дополнительную детектирующую катушку с числом витков (32+32) равным числу витков первичной катушки - Рис. 10 справа. Что и было сделано. При измерении детектирующая катушка действительно выдала большее напряжение чем приложенное к первичной катушке от внешнего генератора.

0x01 graphic

Рис.10 Распределение напряжения (слева) вдоль первичной катушки при сжатии её поля полем вторичной катушкой, и расположение детектирующей катушки (справа), выдающей большее напряжение чем напряжение, приложенное к первичной катушке (при равном числе витков).

Это ещё раз говорит о том, что поле первичной катушки "сжимается" под действием поля вторичной катушки (имеющим противоположную полярность), что приводит к появлению специфического распределения напряжения вдоль первичной катушки.

Далее продолжим экспериментально изучать парадоксы данного преобразователя напряжения, изменив конструкцию и геометрию связанных контуров. Отложим исследованную конструкцию и изготовим другую на основе катушек одинаковой индуктивности, но разной геометрии: одну длинную, а вторую короткую, расположив их рядом вдоль ферритового плоского стержня марки М400 для магнитных антенн, как показано на Рис. 11 внизу. Подключим к катушкам одинаковые конденсаторы по 0,1 мкФ. Затем подключим генератор сигналов (любой формы) и посмотрим осциллограммы для резонансной частоте ї₂. Вид полученных осциллограмм покажем на Рис.11. Слева первичный контур - короткая катушка, справа первичный контур - длинная катушка.

0x01 graphic

Рис. 11 Осциллограммы напряжений на первичном и вторичном контуре. Слева первичный контур - короткая катушка, справа первичный контур - длинная катушка. Красный - первичный контур, жёлтый - вторичный контур.

Как видно из Рис.11, резонансная частота ї₂ при экспериментах оказалась практически одинаковой (около 50 кГц) для обоих вариантах подключения. Что может быть и не удивительно. Но удивительно то, что в обоих вариантах подключения мы получили повышение напряжения (хотя и незначительное). То есть, на результат не влияет какая катушка является первичной, а какая вторичной. В любом случае напряжение повышается. Вот такой парадокс...

В заключении следует сказать, что наблюдаемые парадоксы не противоречат теории радиотехнических цепей и сигналов, а являются лишь увлекательным вариантом её реализации.

ЛИТЕРАТУРА

-- Гоноровский И.С. Радиотехнические цепи и сигналы. Учебник для вуз - ов, 4-е изд., перераб. и доп. - М.: Радио и связь. 1986, 512 с.: ил. ни.

P.S.

1. Рассмотрим соотношение энергий в контурах при резонансном повышении напряжения за счёт различных конденсаторов. Воспользуемся классической формулой для энергии запасаемой в конденсаторе

E _c= CU²/2

Если ёмкость C₂вторичного контура в N раз меньше ёмкости C₁ первичного контура, то, как следует из наших опытов, напряжение на вторичном контуре будет в N раз больше первичного. Следовательно, энергия вторичного контура будет в N раз больше энергии первичного: E_c² =NE_c¹. Так как ёмкость уменьшилась в N раз, а напряжение возросло в N раз.

2. Уменьшая и уменьшая ёмкость во вторичном контуре можно повышать и повышать напряжение на нём, увеличивая запасаемую в нём энергию. При этом, резонансная частота будет расти и расти. То есть, с ростом частоты будет возрастать энергия во вторичном контуре. При этом, энергия в первичном контуре будет оставаться неизменной, так как будет зависеть только от напряжения возбуждения (при отсутствии потерь в контурах).

3. Потери в первичном контуре будут увеличиваться с возрастанием резонансной частоты, что следует из формулы для добротности Q

Q = sqrt (L₁ /C₁) / R

Где R - сопротивление активных потерь, которое не зависит от резонансной частоты. Но от резонансной частоты зависит индуктивность первичного контура L₁, которая будет становиться всё меньше и меньше с ростом частоты (её будет подавлять поле вторичного контура). В результате добротность будет всё меньше и меньше, а потери всё больше. Таким образом пункт (2) справедлив только для случая без потерь, чего на практике не бывает. Добавятся также и потери во вторичном контуре.

4. Эквивалентную схему преобразователя можно представить состоящую из двух различных резонансов: параллельного и последовательного. Параллельный обеспечивает постоянство энергии магнитного поля первичного контура (энергия первичного контура зависит только от напряжения на нём). И последовательный, падение напряжения на ёмкости которого зависит от частоты. В результате на вторичном контуре энергия возрастает с ростом частоты. Хотя, схематически оба контура и первичный, и вторичный являются параллельными.

5. Ситуация с детектирующими катушками не такая простая, как может показаться на первый взгляд. Фактически это вопрос о нарушении третьего закона Ньютона: сила действия равна противодействию. Почему катушки на магнитопроводе показывают, что отклик сильнее воздействия при повышении напряжения, а внешние катушки говорят, что этого нет? Почему так происходит?

ПОЯСНЕНИЯ

Поясним почему детектирующие катушки на магнитопроводе и вне его вели себя по-разному в режиме повышения напряжения.

Начнём издалека, вспомнив чему равна напряжённость магнитного поля H, создаваемого катушкой с током, в зависимости от силы тока I в катушке и числа витков W:

H=IWM

где М - некий коэффициент пропорциональности, зависящий от конструкции катушки.

Откуда следует, что равные напряжённости магнитного поля можно создавать при разном количестве витков катушки. Если сопротивление катушки растёт пропорционально числу витков, то это пропорционально уменьшает ток. Результирующая напряжённость не меняется.

Дале остановимся на варианте используемой катушки. При пояснении нас будут интересовать встречные магнитные поля, как в парадоксальном преобразователе. Для чего катушка должна состоять из двух половин, создающих поля разной направленности. Схему включения половинок выберем параллельную, чтобы по половинкам мог протекать различный ток от одного общего источника.

Начнём с симметричных половинок с малым и большим числом витков. При большом числе витков некая напряжённость будет создаваться за счёт малого тока. При малом числе витков та же напряжённость за счёт большого тока - Рис.12 (А) и (В). При этом, возникающее результирующее поле будет симметричным и одинаковым для обоих вариантов. Убедиться в этом можно на основе датчика Холла (Н). Его показаний будут одинаковыми для разных вариантов и максимальными при расположении датчика точно в середине.

Далее, варианты (А) и (В) объединим, получив вариант (С). При этом напряжённость и симметричность магнитного поля не изменится в силу указанных ранее причин. Все варианты (А), (В) и (С) будут давать одинаковое симметричное магнитное поле равной напряжённости на постоянном токе. Далее перейдём к переменному току - Рис.12 (D).

0x01 graphic

Рис.12 Создание симметричного магнитного поля на постоянном и переменном электрическом токе с помощью различных вариантов катушек, а также расположение детектирующих катушек.

При переходе от постоянного тока к переменному, как в варианте (D), вместо активных сопротивлений катушек на протекание тока будут влиять реактивные сопротивления катушек. Однако, симметричность поля сохраниться, так как малое число витков будет компенсироваться большим током и наоборот. Следовательно, датчик Холла будет показывать максимальное значение точно в середине, как и ранее.

Если в варианте (D) поверх создающих поле катушек намотать детектирующую катушку и поместить её в положение (1), а затем (2), то она покажет ЭДС разной полярности для разных положений (в силу разнонаправленности полей), и разной величины (в силу разного соотношения витков между генерирующими и детектирующей катушкой, как у трансформатора).

Следовательно, при перемещении катушки вдоль оси, можно найти такое положение, когда ЭДС наводимые в ней разными генерирующими катушками будут компенсировать друг друга - Рис.12 (Е). И это положение (3) не будет симметрично относительно генерирующих катушек, так как генерирующие катушки имеют разное число витков.

Таким образом мы пояснили несимметричное расположение детектирующей катушки на магнитопроводе дающей нулевую ЭДС. Но, датчик Холла по-прежнему показывает максимальное значение точно в середине.

Теперь если вместо датчика Холла использовать ещё одну детектирующую катушку, положив её на конструкцию, то получим то, что показано на Рис.12 (F). А если эту детектирующую катушку поставить на ребро, то ЭДС на её выходе станет равной нулю.

Таким образом, детектирующие катушки на магнитопроводе и вне его теперь обе показывают нулевую ЭДС при их различном пространственном положении в данной конструкции.

Аналогичные процессы, но немного сложнее, происходят и в парадоксальном резонансном трансформаторе.

Для тех, кто знаком с классическим электромагнетизмом можно сказать следующее. Детектирующие катушки на магнитопроводе реагируют на электрическую составляющую поля, а вне магнитопровода на магнитную. Вот такой парадокс...

Использованная для экспериментов катушка, показанная на Рис. 12 (F), была намотана на плоском стержне для магнитных антенн и содержала две геометрически равные по длине катушки, но с резко разным числом витков. Для чего одна половина моталась тонким ПЭЛ проводом (чтобы было больше витков), а вторая бифиляром с ПВХ изоляцией (чтобы было меньше витков).

Детектирующие катушки на и вне магнитопровода содержали по 32 витка, что не является принципиальным.

Разработанную конструкцию катушки можно использовать для практических целей, например, для снижения влияния противо ЭДС. Но этот вопрос в данной статье не рассматривается...

Оставить комментарий © Copyright Уткин Владимир (u.v@bk.ru) Размещен: 23/02/2025, изменен: 13/04/2025. 25k. Статистика. Статья: Естествознание Иллюстрации/приложения: 14 шт. Скачать FB2		Ваша оценка:
Аннотация: Предложен подход преобразования напряжения на основе теории связанных резонансных контуров. Приведены структурные и принципиальные схемы. Проведён эксперимент подтверждающий предложенный подход.

Уткин Владимир : другие произведения.

Парадоксальный резонансный преобразователь напряжения