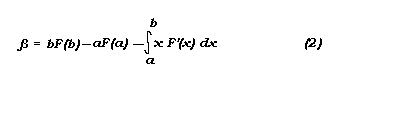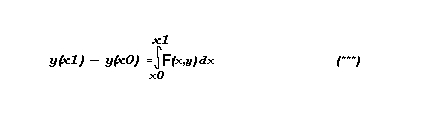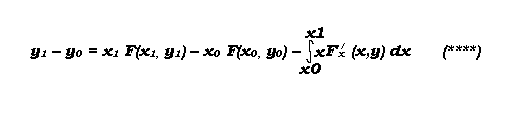Integral = integral +h*fnF(x0+i*h+0.5*h)
Integral = integral +h*fnF(x0+i*h+epsilon*h)
(к сожалению греческая буква эпсилон не на каждом сайте печатается)
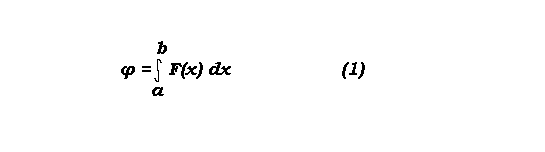
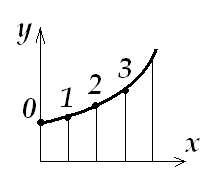
epsilon=const ( 0<= epsilon <=1 )
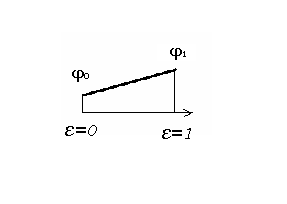
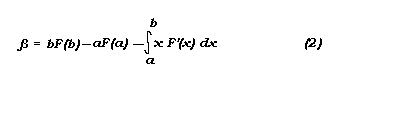
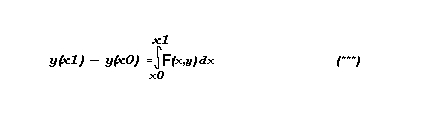
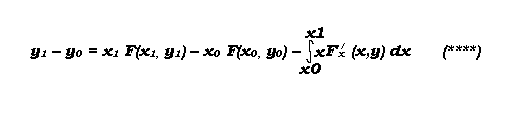
|
|
||
Неплохой новый метод для численного решения обычных дифференциальных уравнений | ||
Integral = integral +h*fnF(x0+i*h+0.5*h)
Integral = integral +h*fnF(x0+i*h+epsilon*h)
(к сожалению греческая буква эпсилон не на каждом сайте печатается)
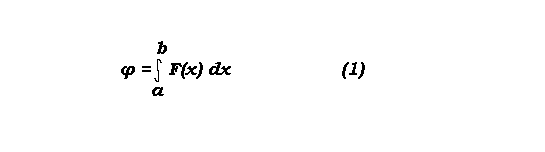

epsilon=const ( 0<= epsilon <=1 )