Путенихин Петр Васильевич. Трёхмерное эллиптическое пространство положительной кривизны. Диск и шар Римана

Оглавление

Предисловие

1. Вращение эллипса на диске Римана

2. Проведение эллипса через 2 точки

Фокусы эллипса

График итерации на диаграмме

Программная итерация

Итерация с прямым перебором угла

Проведение дуги эллипса от точки до точки

3. Фигуры на диске Римана

4. Сфера (шар) Римана

Новые координаты

Автоматические новые координаты

Координаты точки C

Обратное вращение

5. Геометрические тела в сфере Римана

Заключение

Литература

Предисловие

В математике и в физике рассматриваются пространства различного числа измерений и различной кривизны. Наиболее известны три из них: плоские пространства Евклида и искривлённые пространства: пространства отрицательной кривизны Лобачевского и пространства положительной кривизны Римана.

В искривлённых пространствах аналогами прямой линии Евклида объявлены так называемые геодезические или линии наименьших расстояний между точками, наикратчайшие линии. Как правило, построения в криволинейных пространствах заметно более сложны, чем в плоских пространствах Евклида, тем более, в пространствах с числом измерений более двух.

Для упрощения таких построений, в частности, в двухмерном пространстве Лобачевского был разработан Пуанкаре специфический диск, фактически охватывающий бесконечное пространство. На плоский диск проецируется двухмерное искривлённое пространство. Описания какого-либо подобия диска Пуанкаре для трёхмерного пространства Лобачевского в литературе мы не встретили. Наши собственные исследования показали, что такое подобие всё-таки возможно. Мы предложили модель сферы Лобачевского, своеобразного аналога диска Пуанкаре для трёхмерного пространства отрицательной кривизны [5].

Эти же исследования естественным образом подняли вопрос о возможности создания таких же диска и сферы для пространств положительной кривизны Римана. И в этом случае выяснилось, что такие системы возможны. Мы дали им очевидное наименование - диск и сфера (шар) Римана. Следует заметить, что название "диск Римана" не совсем верно. Дело в том, что под диском подразумевается круг, имеющий толщину. Правильнее говорить "круг Римана", подчёркивая этим, что объект толщины не имеет. Однако мы будем придерживаться традиционных обозначений и не будем без особой необходимости противопоставлять диск кругу, а шар - сфере.

Очевидно, что предложенный диск Римана можно рассматривать как своеобразную проекцию сферы на плоскость. Как и сфера, диск описывает лишь ограниченную область пространства, занимаемого кругом соответствующего радиуса. Поскольку геодезическими на сфере являются большие круги, на диске их проекциями и, соответственно, геодезическим становятся проекции кругов - эллипсы.

Геометрические построения произвольных криволинейных фигур на диске Римана не имеют никаких сложностей. Напротив, для геометрических построений на таком диске с использованием геодезических, эллипсов возникает необходимость их корректного построения с предопределёнными характеристиками. Главной задачей в этом случае становится необходимость проведения геодезической, эллипса, наикратчайшей линии через две произвольно заданные точки. Решение этой задачи приводится в первой части данной работы.

Во второй части мы рассматриваем сферу (шар) Римана - специфическую эмуляцию трёхмерного пространства положительной кривизны Римана. В литературе и в интернете мы не встретили никаких упоминаний о возможности таких построений. Как правило, рассматриваются лишь двухмерные пространства положительной кривизны, поверхности сфер.

Трёхмерное пространство положительной кривизны мы поместили в шар конечных размеров. В отличие от диска Римана, в шаре все объекты имеют теперь уже явные три координаты. Положительная кривизна пространства привела к тому, что здесь, как и в сфере Лобачевского, появился новый класс геодезических - геодезические поверхности, двухмерные пространства. В их качестве естественным образом выступили эллипсоиды с двумя равными осями, то есть, сфероиды.

1. Вращение эллипса на диске Римана

На начальном этапе исследования диска Римана рассмотрим основную задачу на построение эллипсов: проведение эллипса через две произвольно заданные точки [1]. Эти две точки образуют треугольник с вершиной в начале координат. Задачу такого построения можно выполнить в два этапа: построить базовый эллипс, то есть, эллипс с полуосями, совпадающими с осями координат, и проходящего через треугольник, подобный треугольнику, заданному исходными точками. После этого эллипс можно повернуть до его прохождения через эти заданные точки. Для осуществления второго этапа рассмотрим соответствующую задачу - вращение какого-либо базового эллипса на диске. Рассматриваем только эллипсы, имеющие большую полуось, равную радиусу диска Римана. Сформулируем задачу.

Итак, у нас задан диск Римана, круг радиуса R, в котором нарисован эллипс с большой полуосью a = R, расположенной горизонтально, и с произвольной малой полуосью b. Требуется повернуть этот эллипс вокруг центра круга на произвольный угол φ. Каноническое уравнение эллипса имеет вид

Для решения поставленной задачи нам понадобятся как это каноническое (1.1), так и параметрическое уравнения эллипса

Рассматривать будем только верхнюю половину эллипса, рассчитывая в дальнейшем отнести её к классу геодезических в рамках пространства некоторой окружности. Этот выбор мы обосновываем тем, что в системе координат Земли, на сфере рассматриваются обычно не большие круги целиком, а только их половины - меридианы.

Результат поворота эллипса будем фиксировать по перемещению некоторой точки C, закреплённой на построенном исходном, базовом эллипсе. Проведём к этой точке линию, вектор из центра круга. Для определённости назовем эту линию 0C радиусом C эллипса, подразумевая его полное название - радиус-вектор эллипса в точке C. Согласно параметрическим уравнениям эллипса, координаты точки определяются системой

При заданных координатах точки C три других параметра оказываются взаимосвязанными. А именно: для рассматриваемого нами варианта описанной окружности радиуса R, равного большой полуоси эллипса, однозначно определёнными становятся малая полуось эллипса и угол наклона вектора C. При вращении эллипса все его точки, в том числе и C, останутся на неизменном удалении от центра. Как видим на рисунке рис.1.1, линия эллипса при его параметрическом построении образуется движением некоторой точки G по внешнему радиусу круга. При этом координаты точек эллипса образуются как проекции двух разных окружностей. Можно заметить, что при инверсной комбинации проекций будет построен ортогональный эллипс.

Квадрат длины введённого радиус-вектора C равен

Угол α назовём углом радиуса C. Величину угла определим из соотношения

Для поворота эллипса вокруг центральной точки на некоторый произвольный угол φ, вычислим координаты всех его точек как проекции всех повернутых радиусов эллипса.

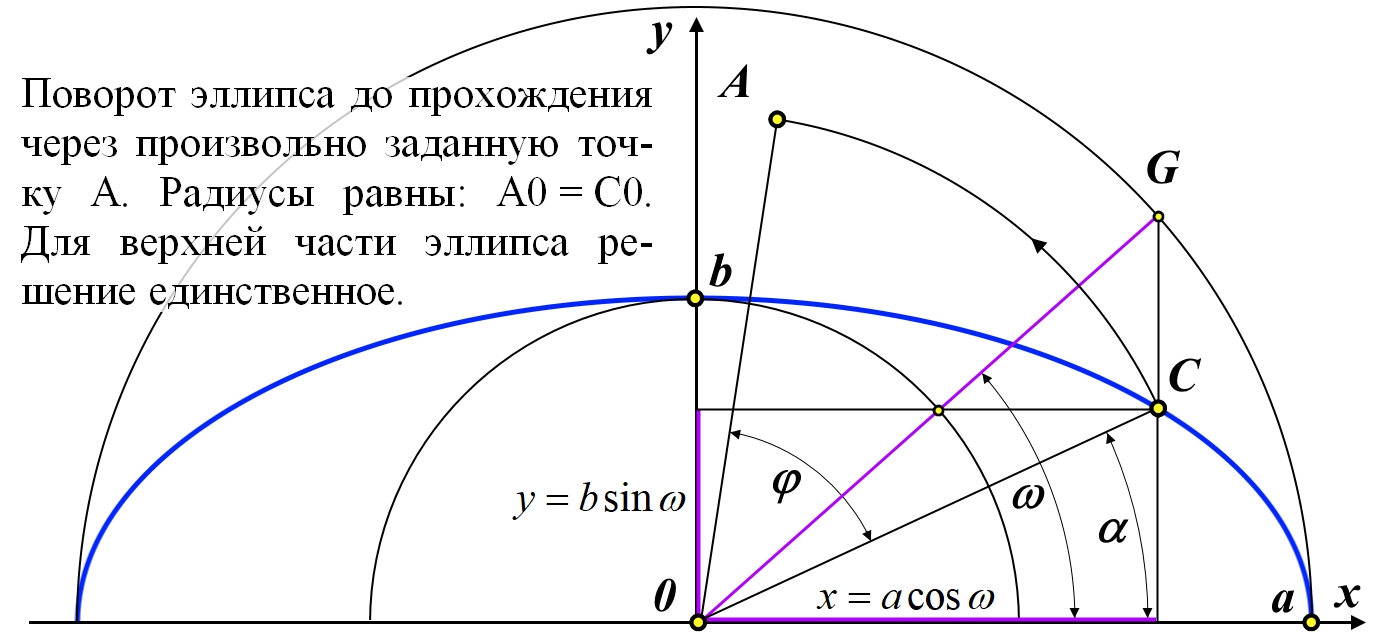
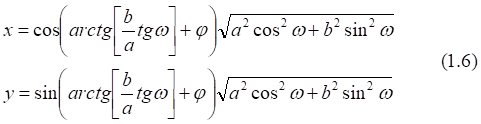
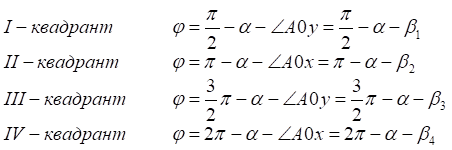
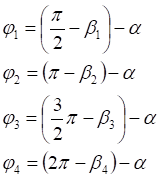
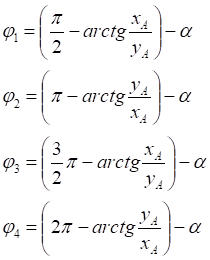
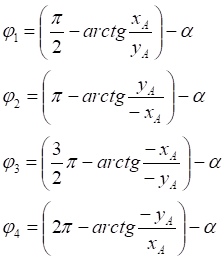
ellipse

Рис.1.1. Поворот эллипса до прохождения через произвольно заданную точку A. Радиусы равны: A0 = C0. Для верхней части эллипса решение единственное.

В результате такого поворота на угол φ, координаты точки C изменятся, то есть перейдут в некоторую пока неизвестную нам точку A:

Решим эту систему совместно с уравнением (1.3)

Подставим в систему значение найденного угла α из (1.4), в результате чего получим новую систему, содержащую только переменный параметр ω и известные величины

ellipse

Полученная параметрическая система позволяет повернуть эллипс с полуосями (a = R, b) на произвольный угол φ. На следующе рисунке представлены эллипсы, повёрнутые на разные углы с помощью полученной системы уравнений

ellipse

Рис.1.2. Эллипсы, образованные программным поворотом основного эллипса (красного) на разные углы

Сформированная система уравнений позволяет повернуть эллипс на любой угол. Но она также позволяет решить и обратную задачу: определить угол поворота, при котором эллипс пройдёт через заранее заданную произвольную точку.

Очевидно, что через любую точку в пределах рассматриваемого круга можно провести неограниченное число эллипсов, различающихся малой полуосью. Поэтому мы рассмотрим более жёсткие условия, частный вариант эллипса, у которого задана также и вторая полуось. Можно заметить, что таких эллипсов, проходящих через одну точку в круге, существует только два, поскольку эллиптическая кривая замкнута, буквально, имеет две стороны. Поэтому для определённости, однозначности выше мы решили рассматривать только половину эллипса, его верхнюю дугу.

Легко заметить, что эллипс с указанными характеристиками может пройти только через точки, находящиеся в области кольца, образованного его радиусами.

ellipse

Рис.1.3. Вращение эллипса до совмещения с произвольно выбранной точкой A. Определение параметров углов целевой точки A.

Процесс вращения означает движение по дуге точки C эллипса в точку A. Длина радиуса C0 при этом равна длине радиуса A0

Угол φ между векторами в уравнениях (1.6) - это искомый угол, на который нужно повернуть эллипс для его прохождения через точку A. Очевидно, этот угол зависит от того, в каком квадранте находится точка A. Действительно, для каждого из квадрантов запишем

ellipse

Эти разнообразные определения угла φ желательно свести к некоторой единой системе. Для создания такой системы изменим запись уравнений. Для всех четырёх квадрантов получаем

ellipse

Для определения характеристик углов β, расшифруем их, представим в координатах соответствующих точек A

ellipse

Далее для наглядности пометим значками минуса отрицательные координаты. Подчеркнём, в данном случае эти значки просто обозначают, что соответствующая координата имеет отрицательное значение

ellipse

Из этих расшифровок выводим условия использования той или иной строки определения угла в скобках:

1. x > 0, y > 0

2. x < 0, y > 0

3. x < 0, y < 0

4. x > 0, y < 0

Теперь мы должны взять положительные значения, модули дробей под функциями арктангенса

ellipse

С учётом модулей под знаками арктангенсов введём новые обозначения. Углы β, представленные арктангенсами, в уравнении разные, поэтому обозначим их индексами, означающими, какая координата в дроби под арктангенсом находится сверху, а какая - снизу.

ellipse

Уточним: в данных уравнениях верхний и нижний индексы при β не имеют обычного математического смысла, это просто метки, что в соответствующей функции арктангенса числителем и знаменателем являются координаты, занимающие соответствующее индексу место.

Поскольку координаты точки A заданы условиями задачи, этот угол β также однозначно определён. Второй угол - α позволяет определить значение параметрического угла ω, при котором и образуется вращаемый вектор C0. Рассмотрим каноническое уравнение эллипса

После преобразований получаем

ellipse

Используем это уравнение в условии равенства исходного радиуса C0 и радиуса A0, в который он должен переместиться

Преобразуем

ellipse

Из уравнений (1.10) и (1.9) находим вторую координату

ellipse

Уравнения (1.11) и (1.12) содержат только известные величины, поэтому из них мы можем найти искомый угол α

ellipse

Преобразуем

Упростим выражение в числителе под корнем

ellipse

Подставляем в предыдущее, исходное уравнение

На рисунке рис.1.3 можно увидеть, что в общем случае, для всех вариантов расположения точки A для i = 1...4 справедливо равенство, из которого находим угол φ

ellipse

Сравниваем это выражение с (1.8) и исправляем последнее

ellipse

Подставляем вычисленные параметры и определяем искомый угол поворота φ

Используя это уравнение угла, мы можем повернуть исходный эллипс с полуосями (a = R, b) до прохождения его через заданную точку A. На следующем рисунке представлены два примера таких вращений

ellipse

Рис.1.4. На исходном эллипсе выбрана произвольная точка С. Эллипс (верхняя половина) повёрнут вокруг своей центральной точки так, что в новых положениях точка C совместилась с точкой A или с точкой B. Радиусы точек равны: C0 = A0 = B0

2. Проведение эллипса через 2 точки

Все эллипсы, формируемые в дальнейших рассуждениях, как и в рассмотренной задаче, имеют одинаковую большую полуось, поэтому все построения по-прежнему рассматриваем как построения в рамках круга, имеющего радиус большой полуоси этих эллипсов. Мы рассмотрели вращение эллипса с заданными, фиксированными полуосями с тем, чтобы эллипс прошёл через произвольную, также заданную точку. Далее мы ставим цель провести эллипс теперь уже через две произвольно заданные точки.

Для решения этой задачи, рассмотрим предварительный вариант. В этом варианте мы не устанавливаем значение малой полуоси эллипса, а попытаемся определить её зависимость от точки, через которую эллипс должен пройти. Иначе говоря, проведём разные эллипсы через единственную заданную точку. Эту произвольную точку A зададим уравнением

Радиус-вектор R_A - это удалённость точки A от центра эллипса. Повторим, что точка обязательно должна находиться в кольце эллипса, то есть, радиус А0 должен быть больше малой полуоси и, понятно, меньше большой полуоси эллипса. Для построения эллипса используем параметрические уравнения (1.2)

Полуоси этого эллипса, который мы называем базовым, расположены вдоль осей координат. Выбираем значения полуосей (а = R, b) и строим эллипс, показанный на рис.1.1. На рисунок нанесены необходимые для вычислений вспомогательная точка C, которая находится на линии эллипса, и целевая точка A.

Напомним, что линию 0C мы назвали радиусом R_C эллипса, полное название - радиус-вектор эллипса в точке C. Соответственно, угол α назван углом радиуса C. Для вращения эллипса мы разработали систему параметрических уравнений (1.6, 1.15) для эллипса с заданной большой полуосью a = R и варьируемой малой полуосью b = r. Путём вращения эллипс проводится через некоторую, произвольно заданную точку A. Угол вращения φ определяется координатами этой точки.

Сущность проведения эллипса через произвольную точку A можно описать следующим образом. Сначала мы строим некоторый фиксированный произвольный базовый эллипс (a = R, b) с горизонтально расположенной большой полуосью и произвольно выбранной малой полуосью b. После построения такого исходного эллипса мы вращаем его вокруг центра до совмещения с точкой A. Понятно, что такое решение, как и в предыдущем варианте, фактически определяет бесконечное множество разных эллипсов, различающихся малой полуосью. Просто меняя величину малой полуоси, мы получим соответствующие разные эллипсы, проходящие через заданную точку. Поскольку каждый эллипс может пройти через эту точку одной из двух своих сторон, мы рассматриваем только одну их сторону. Этот выбор ранее мы обосновали тем, что в системе координат Земли, на сфере рассматриваются обычно не большие круги целиком, а только их половины - меридианы. На следующем рисунке изображены такие разные полу-эллипсы, проходящие через заданную точку A

ellipse

Рис.2.1. При изменении малой полуоси исходного, синего полу-эллипса и неизменной большой, эллипс вращается и пересекает всю область круга. Полу-эллипс может пройти через две точки - A и какую-либо произвольную вторую точку M. На последнем рисунке видно, что исходный эллипс не может иметь малую полуось, длиннее вектора A0

Как видим, красный полу-эллипс всегда проходит через выбранную точку A (красный вектор) независимо от величины его малой полуоси. Синим цветом выделен "базовый" эллипс, верхняя его часть, вращением которого и была образована верхняя часть красного эллипса.

Можно сказать, что на всех рисунках изображён один и тот же эллипс в разных положениях, и у которого малая полуось вытягивается. Замечаем, что соответствующий II-квадрант такого обобщённого эллипса, его условно левая верхняя четверть, полностью пересекает зону II-квадранта системы координат. Это значит, что при некотором значении его малой полуоси эллипс пройдёт через любую наперёд заданную вторую точку в этом квадранте. На последнем рисунке видно, что при меньшей полуоси эллипса большей, чем радиус точки A, решение отсутствует.

Фокусы эллипса

В рассмотренном предварительном варианте прохождение эллипса через некоторую вторую точку обеспечивается простым перебором, подбором длины его малой полуоси. Далее мы определим точное значение малой полуоси, для обеспечения такого пересечения второй точки.

Изменим рисунок рис.1.1 для определения параметров теперь уже двух вспомогательных точек C и D. Как и ранее, мы должны определить угол поворота этого эллипса, чтобы вспомогательные точки C и D совместились с другими произвольными точками, соответственно, A и B (на рисунке не показаны). При этом мы заранее устанавливаем равенство радиусов R_A = R_C и R_B = R_D. Кроме этого, очевидно ещё одно равенство - угол между C и D равен изначально заданному углу между A и B. Угол этот обозначим символом γ. На следующем рисунке это угол C0D.

Параметры вспомогательных точек определяем, используя параметр эллипса - фокус F.

ellipse

Рис.2.2. Проведение эллипса с известной большой полуосью через две заданные точки C и D или построение эллипса по двум (фактически - по трём, считая полуось) заданным точкам

Взаимосвязь параметров - фокуса F и точек C и D через длины их векторов описывается уравнением

Знаки модулей отрезков здесь не используем, поскольку это лишь их обозначения. Вычислим длины этих отрезков. Рассматриваем для первой точки C два прямоугольных треугольника F₀С_xС и F₁С_xС. Отрезки F₀С и F₁С являются гипотенузами этих треугольников, поэтому

ellipse

Из вычислений в предыдущей главе берём некоторые величины и делаем очевидную подстановку, замену F = F₀ = -F₁

Разносим величины с квадратными корнями по разные стороны от знака равенства и возводим в квадрат

Сокращаем

Перегруппируем слагаемые и вновь возводим в квадрат

Получаем окончательное выражение

По аналогии записываем уравнение для второй точки D

По заданным условиям задачи о 2-точках, у нас есть возможность определить связь между C_x и D_x, поскольку нам известен угол γ между векторами C0 и D0. В самом деле, ранее мы обозначили угол наклона вектора C0 символом α, поэтому находим

ellipse

Соответственно, инверсный вариант этого уравнения, то есть, определение C_x как функции от D_x, имеет вид

Угол γ между векторами C и D для полученных уравнений определим, используя известные параметры заданных целевых точек A и B

Запишем кратко оба эти взаимосвязанные, инверсные уравнения

ellipse

Выведенные уравнения (2.1), (2.7) и (2.2) представим в виде компактной системы уравнений

ellipse

Замечаем, что система описывает множество эллипсов, проходящих через точку C, и имеющих разные фокусы F. Действительно, задаём некое произвольное значение фокуса F и из нижнего уравнения (2.8) находим соответствующее ей значение абсциссы точки C

ellipse

По некоторому, произвольно заданному значению фокуса F определяем длину малой полуоси эллипса

По известному значению длины радиуса R_C находим для справки вторую координату точки C

Меняя значения фокуса F, строим эллипсы, проходящие через заданную точку C

ellipse

Рис.2.3. Эллипсы с разными фокусами F, проходящие через точку C, удалённую о центра на расстояние R_C

Поскольку через точку C с радиусом R_C мы можем провести любое количество эллипсов; очевидно, что какой-то из этих эллипсов обязательно пройдёт и через вторую точку - D с радиусом R_D. Как и для точки C условием такого прохождения является соответствие точки D таким же условиям, что и C, то есть для точки D должно выполняться уравнение (2.3)

Из этого уравнения находим x-координату точки D и затем по длине этого вектора его y-координату

ellipse

Здесь мы сразу же учли, что длина вектора D равна по условиям задачи длине вектора B. Однако мы нашли, определили две точки для эллипса с произвольно выбранным фокусом F. Это означает, что угол между векторами C и D может быть любым, поскольку он явно определяется величиной фокуса. Действительно, согласно уравнениям (2.4) и (2.5) угол γ между векторами равен

ellipse

а проекции D_x и C_x, согласно уравнениям (2.9) и (2.12), однозначно определяются величиной фокуса F. И здесь мы замечаем ещё одну важную связь, исключающую множественность решений. Это предопределённость угла γ между векторами C и D. Согласно условиям задачи, этот угол задан равным углу между векторами A и B (2.6). Следовательно, мы можем выбрать только одно значение фокуса F, значение, при котором между векторами C и D будет образован именно этот, заданный условиями задачи угол γ.

Описанные условия предопределяют последовательность построений. Сначала произведём построения, что называется, вручную, демонстрационно. Для этого изобразим на рисунке рассмотренную картину построения эллипса, проходящего через две рассмотренные точки C и D, определённые их радиус-векторами R_C и R_D и углом γ между ними. Нам необходимо убедиться, что такое решение существует и оно - единственное. Обратимся к следующему рисунку

ellipse

Рис.2.4. При повороте эллипса на угол φ, точки C и D на нём совместятся с точками A и B, соответственно. Углы A0B и C0D равны.

Анализируя уравнения (2.7) - (2.9) и (2.12) как систему, приходим к выводу, что простого аналитического решения система, видимо, не имеет. Переменные связаны друг с другом не только квадратичными функциями, но и тригонометрическими - косинусом и арктангенсом. С другой стороны, все переменные явно выражены друг через друга, что позволяет образовать простую итерационную цепочку даже для ручных вычислений.

Для такого упрощённого итерационного построения эллипса используем уравнения (2.9) и (2.12). Плавно уменьшаем фокус F от ~ 9 до ~ 8,01 и каждый раз заново строим фигуры. В результате добиваемся того, что углы A0B и C0D сравнялись. Если теперь повернуть эллипс на угол φ, то точки C и D на нём совместятся с точками A и B. Такую процедуру можно назвать итерацией, правда "на глазок". Очевидно, что она не только медленная, но и неточная. Вместе с тем, эти же уравнения позволяют осуществить и более корректное и точное программное итерационное построение.

График итерации на диаграмме

Для отладки итерационного процесса, для его наглядного контроля, удобно использовать соответствующий процессу график изменений фокуса. Поскольку число итераций мы выбрали достаточно большим, порядка 3 000, возникли сложности в VBA Excel: такое большого количество точек на графике отразить оказалось сложно, фактически невозможно. Поэтому в график следует выводить не все точки, а только некоторые на этом интервале.

Если итерация быстрая, то итог будет получен буквально на первых шагах, и график будет иметь вид тонкого пика. Следовательно, желательно использовать неравномерную шкалу номеров итераций. Очевидной является экспоненциальная шкала. При наших настройках предельному значению, например, n = 3000 должна соответствовать координата с номером на диаграмме m = 20. Коэффициент экспоненциального преобразования в этом случае определим из уравнения

Здесь n_i - номер текущей, i-той итерации; m - предельное значение шкалы графика; k - параметр, связывающий эти две величины. В таблицу данных мы выводим не все значения фокуса, а только значения с некоторым интервалом.

Программная итерация

Сначала отметим, что рассмотренная задача является, по существу, обратной. На самом деле, точки C и D являются произвольными лишь методически, то есть, они полностью предопределены параметрами действительно произвольных точек A и B. Конечной целью преобразований является проведение эллипса именно через эти точки A и B. Цель достигается вращением вспомогательного, базового эллипса, проведённого через предопределённые точки C и D.

Для автоматического, программного построения эллипса по двум точкам, здесь это C и D, у нас есть все необходимые данные. Задан предопределяющий угол A0B между векторами A0 и B0, к которому нам необходимо привести угол C0D

Для построения задаём некое исходное, предельное значение фокуса - Fi = R. По этому значению фокуса, используя уравнения (2.9) и (2.11), вычисляем координаты точки C

ellipse

Сразу же определяем малую полуось (2.10)

По значению угла A0B = γ между векторами из (2.13) и из соотношения (2.4), связывающего координаты C_x и D_x, определяем значение координат точки D

ellipse

Далее, теперь уже по вычисленному значению координаты D_x вычисляем из (2.3) новое значение фокуса F

Проверяем, насколько изменилось значение фокуса. Если изменение мало, то считаем их равным

После этого совпадения вычисляем окончательные значения координат и малой полуоси эллипса. Замечено, что итерация достаточно быстрая. В рассмотренном варианте уже через 10-12 шагов было достигнуто приемлемо точное решение.

Итак, мы получили сначала вручную, затем программно главные параметры "базового", предопределённого эллипса - значения его полуосей. Теперь определяем угол его поворота, после чего - поворачиваем. Угол, на который нужно повернуть эллипс определяется просто

Проверяем, пройдёт ли через точки A и B этот построенный эллипс, при его повороте на угол φ. Для проверочных построений используем уравнения вращения эллипса (1.5)

Как видим, после поворота эллипс на обоих рисунках прошёл точно через две целевые точки A и B. Для наглядности на этот рисунок мы снизу добавили график итерации (красный), показывающий, как в процессе итерации фокус F приближается к своему окончательному значению - синяя линия.

ellipse

Рис.2.5. При вращении базового, синего эллипса, его точки C и D совмещаются с произвольно заданными точками A и B на эквивалентном красном эллипсе. Рисунки слева и справа различаются координатами точек назначения A и B. Точки C и D - производные. Внизу рисунков - графики итерации, показывающие число итераций, вычислений для достижения нужного значения фокуса F

Заметно, что в варианте вращения рис.2.5b уже после 7-го шага изменяемое, подбираемое значение фокуса, красная ломаная сливается с итоговой, синей прямой. Этого количества шагов оказалось достаточно, чтобы вычислить действительное значение фокуса. Проведём ещё один процесс вращения, с другими значениями углов и радиусов. Как видно на рис.2.5a, в этом варианте итерационных шагов оказалось заметно больше, порядка сотни. Тем не менее, значение фокуса вычислено достаточно быстро.

Итерация с прямым перебором угла

В предыдущем варианте при его визуальной эффективности были выявлены проблемы. Обнаруживались пары точек, через которые эллиптическая дуга не проходила. Для устранения проблемы и дальнейшего упрощения алгоритма было решено использовать простой последовательный рост угла производных векторов. За определяющий выбираем один из векторов, независимо от первенства по углу. Пусть это будет вектор C. У вектора D угол визуально может быть ближе или дальше, если он намного опережает угол С.

Организуем цикл роста угла C от нуля до 180 градусов, его предельного значения. Для каждого значения угла строим соответствующий базовый эллипс, его верхнюю дугу. Угол вектора D однозначно определяется углом между векторами A и B. Поэтому для него также строим эллипс. Оба эллипса строим, определив по уравнениям (2.2) и (2.3) их фокусы, а затем и малые полуоси.

Рост угла вектора C приводит к тому, что эти два эллипса начинают сближаться. Величину прироста угла C берём равной некоторой доле от разницы малых полуосей этих двух эллипсов. Это приводит к тому, что при сближении малых кругов этих эллипсов шаг прироста угла C уменьшается, повышая точность построения.

Вместе с тем, в процессе возникла, по сути, очевидная проблема. Иногда эллипсы сливались, но точка D оказывалась на нижней половине, нижней дуге своего эллипса, на половине, от которой мы решили отказаться. Решением проблемы было продолжение роста угла C после первого, зеркального слияния эллипсов. Признаком первого, зеркального слияния было то, что вектор D находился в IV-ом квадранте. Поэтому после достижения первого совпадения эллипсов, процедура продолжается. Длительность итерации не превышала нескольких секунд. В конечном счете, главный результат был достигнут: проведение эллипса через любые две произвольные точки.

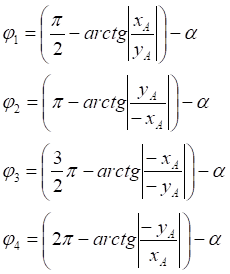
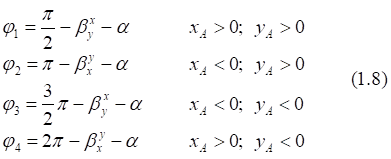
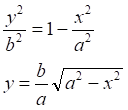
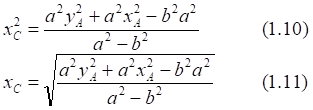
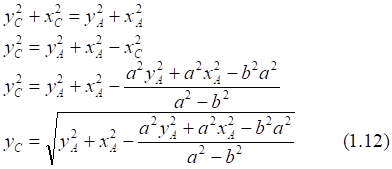
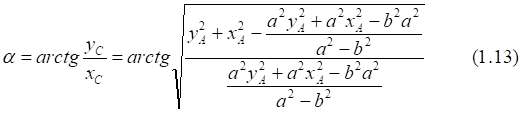
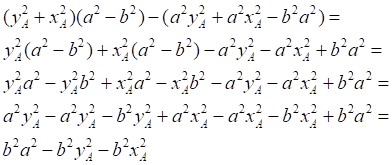
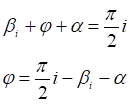
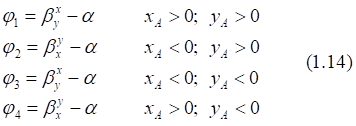
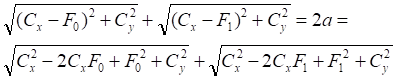
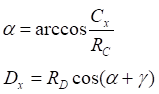
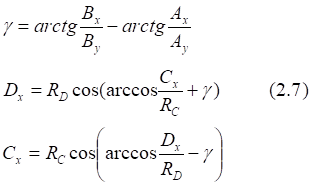
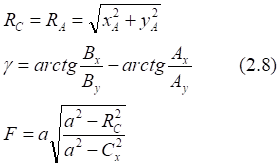
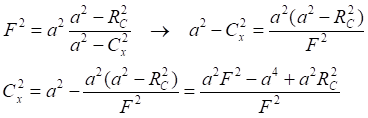
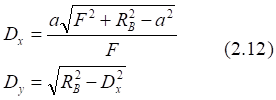
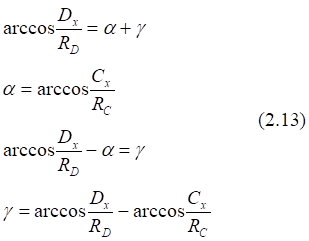
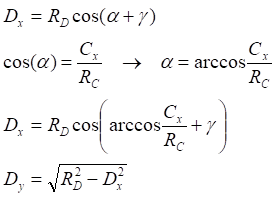
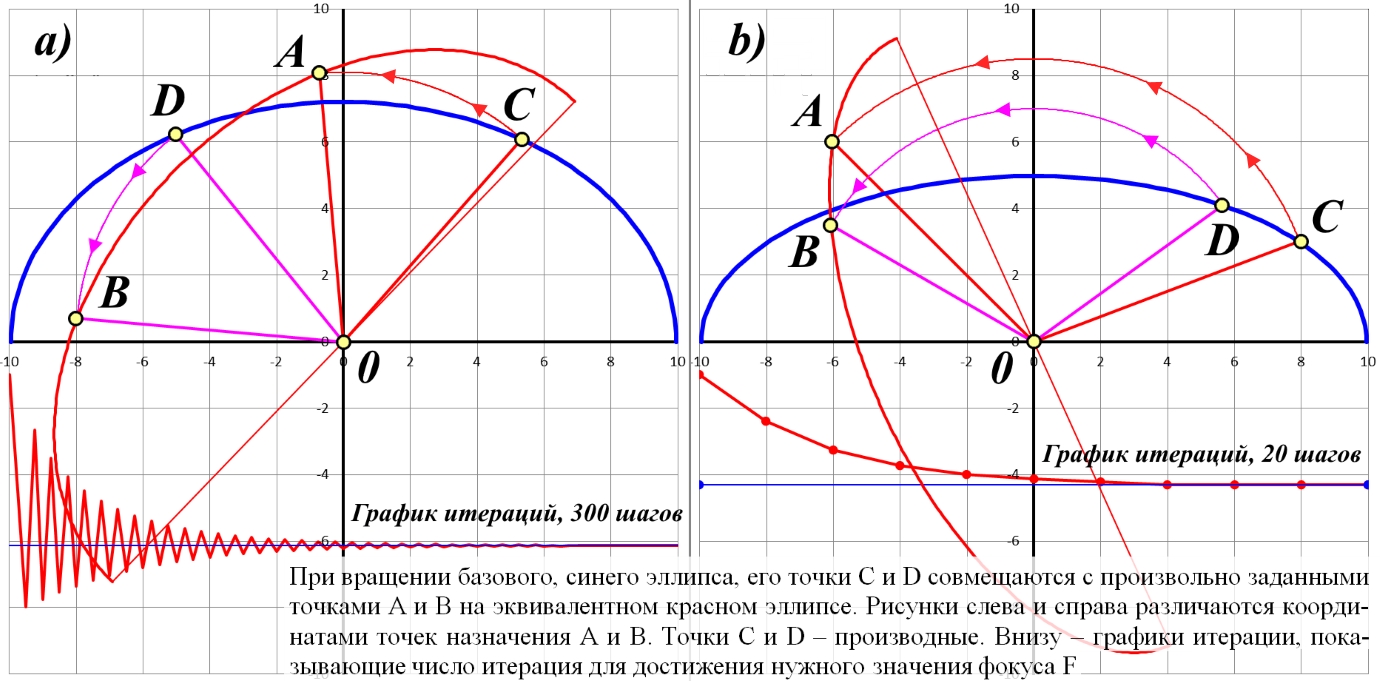
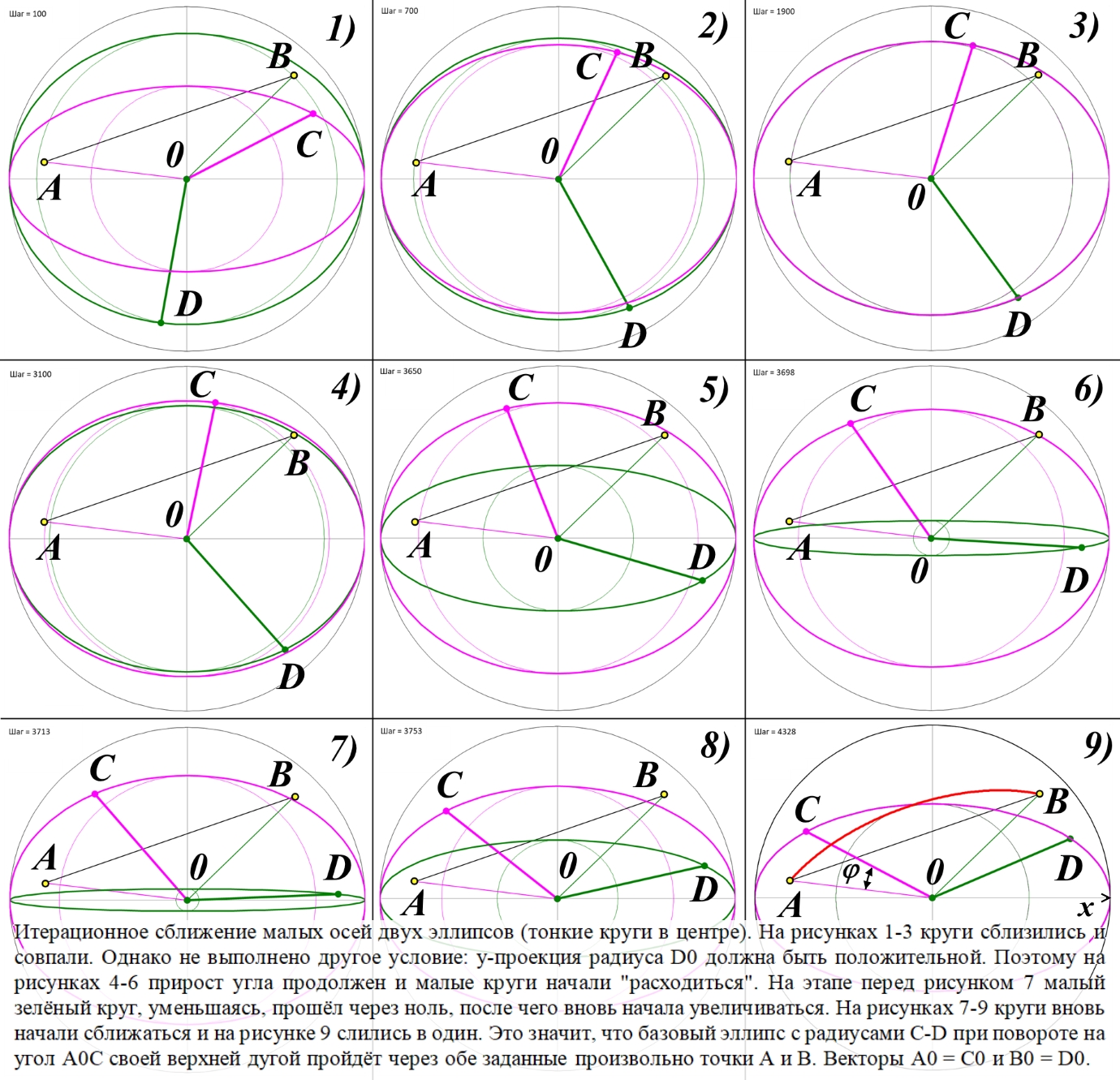
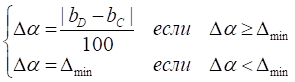
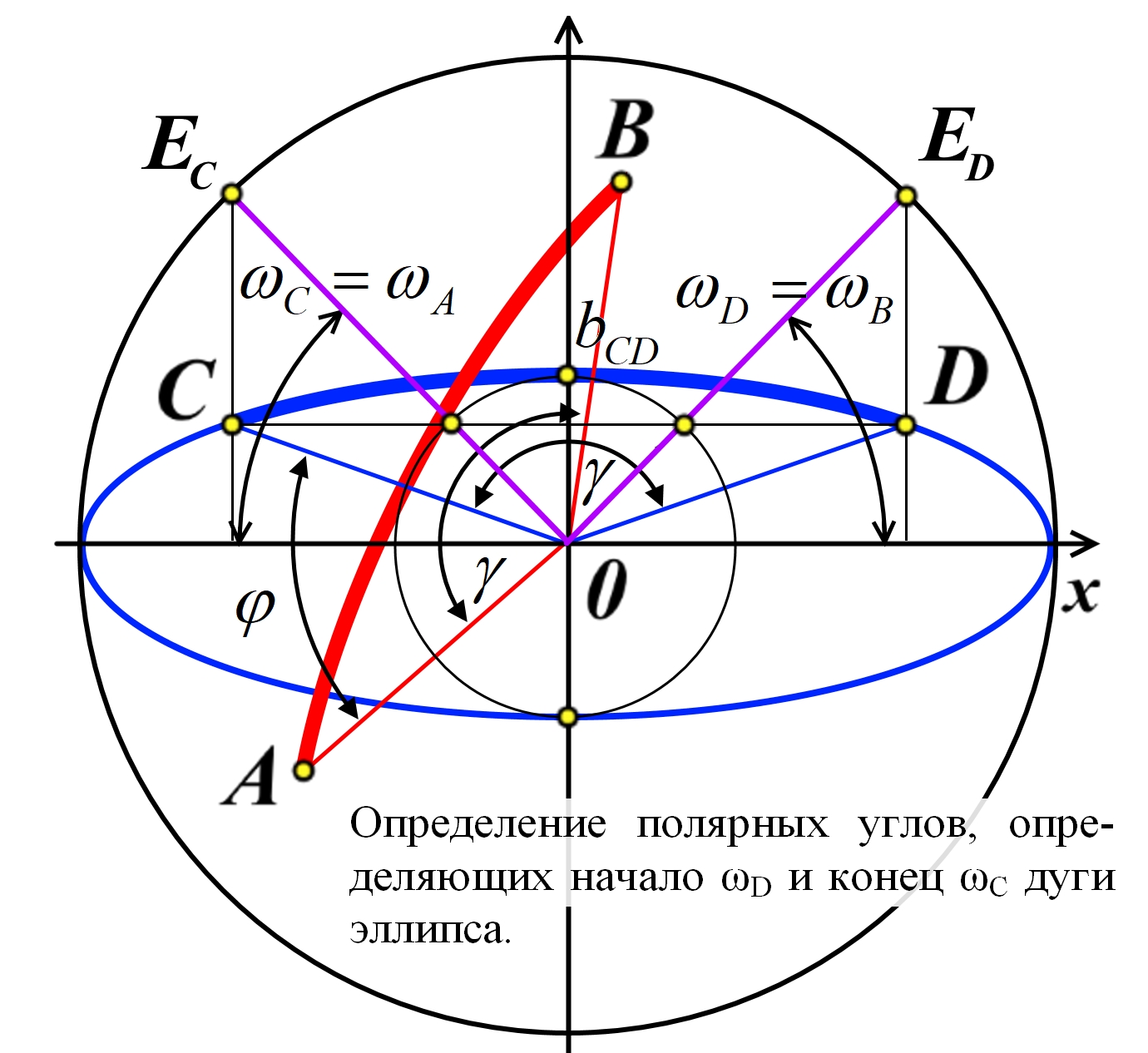
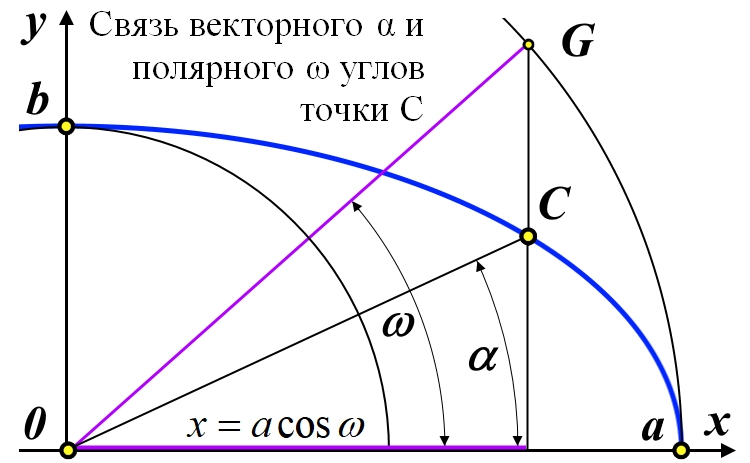
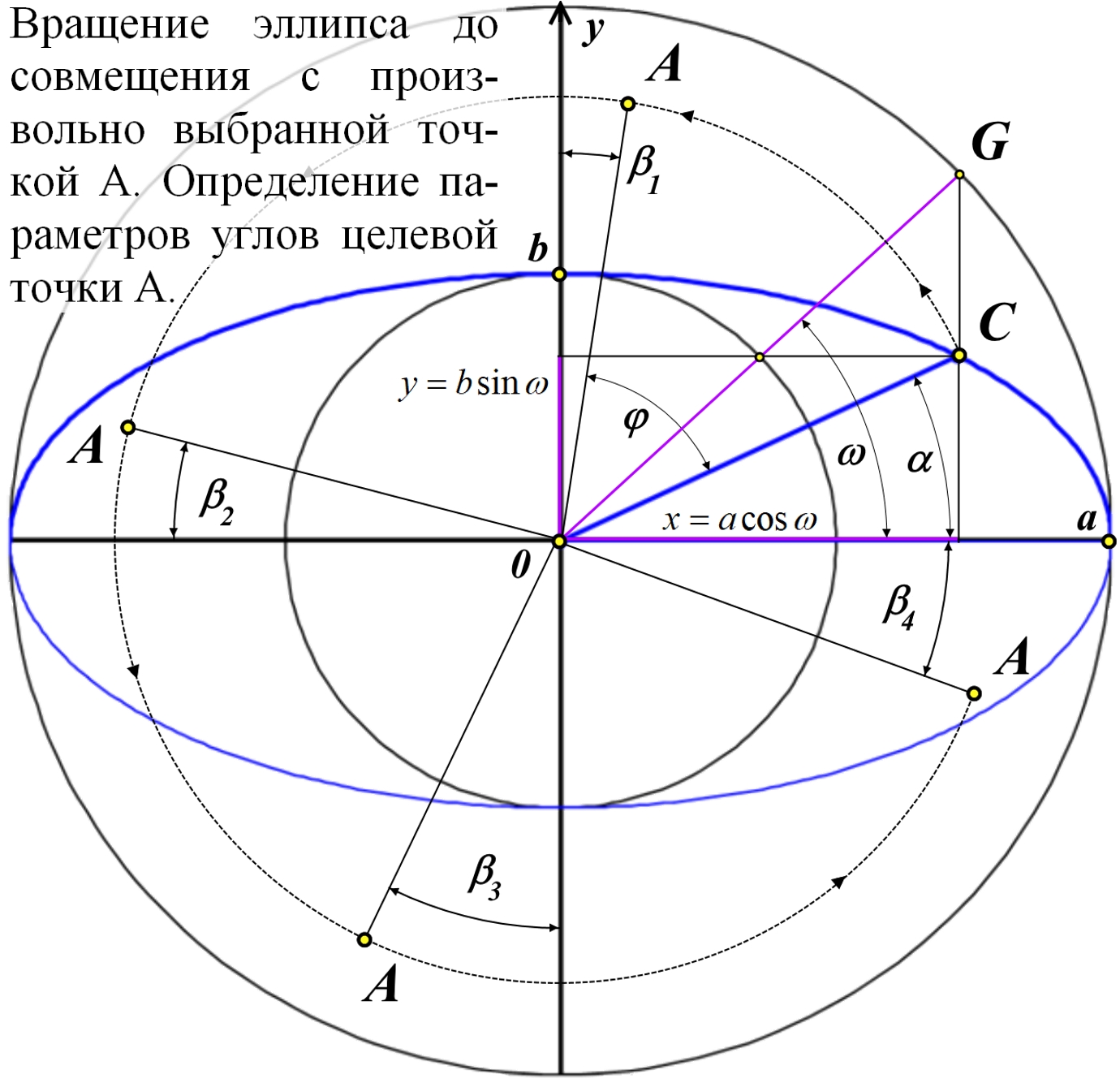
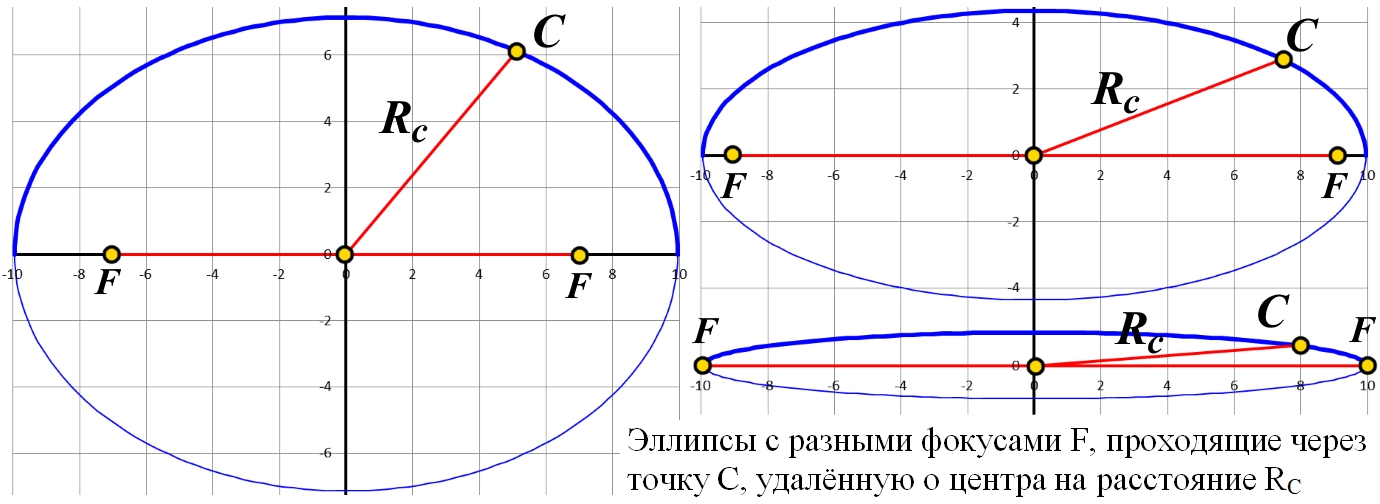
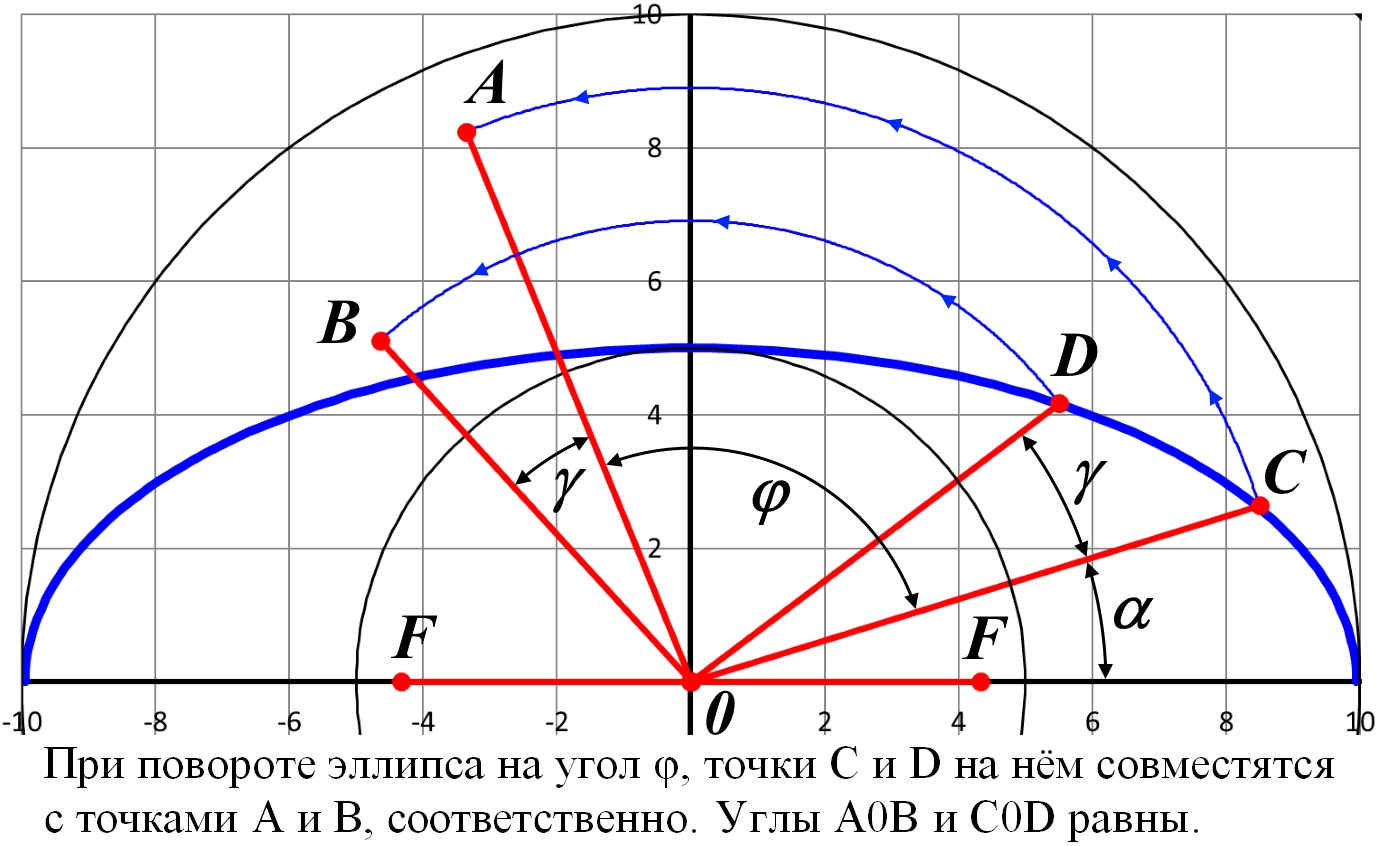
ellipse

Рис.2.6. Итерационное сближение малых осей двух эллипсов (тонкие круги в центре). На рисунках рис.2.6.1-3 круги сблизились и совпали. Однако не выполнено другое условие: y-проекция радиуса D0 должна быть положительной. Поэтому на рисунках рис.2.6.4-6 прирост угла продолжен и малые круги начали "расходиться". На этапе перед рисунком рис.2.6.7 малый зелёный круг, уменьшаясь, прошёл через ноль, после чего вновь начала увеличиваться. На рисунках рис.2.6.7-9 круги вновь начали сближаться и на рисунке рис.2.6.9 слились в один. Это значит, что базовый эллипс с радиусами C-D при повороте на угол A0C своей верхней дугой пройдёт через обе заданные произвольно точки A и B. Векторы A0 = C0 и B0 = D0.

Приведём более подробное описание процесса итерации. Проводим радиус-вектор базового эллипса C0 под углом α = 0 и радиус D0 - под отстающим углом γ к радиусу C0. Если проекция радиус-вектора D_x < 0, даём некоторый небольшой прирост углу α. Величину прироста угла задаём пропорциональной разнице длин полуосей

Здесь делитель 100 - произвольная величина, выбранная наугад. Можно взять и 10, и 1000, что по опыту влияет лишь на время выполнения процедуры, причём довольно незначительно. По уравнениям (2.2) и (2.3) вычисляем малые полуоси двух разных эллипсов - b_C и b_D. Строим эти два эллипса на диаграмме, для наглядности, визуализации. После прироста угла α вновь вычисляем текущие значения полуосей b_C и b_D и их разницу. Если разница больше некоторой заранее заданной предельной величины, точности совпадения Δb > Δ_min, увеличиваем значение α и вычисляем новые значения полуосей эллипсов. В процессе роста угла визуально круги полуосей b_D и b_C и эллипсы D0 и C0, построенные на них, сближаются, а величина прироста угла Δα - уменьшается. Когда сближение завершается слиянием эллипсов, цикл прекращается, но только при условии D_y > 0. В противном случае, если D_y < 0, мы заметим, что на совпавших эллипсах точки C и D лежат на разных дугах суммарного, слившегося эллипса: точка C - на верхней дуге, D - на нижней. Поскольку по условиям задачи нижнюю дугу мы отбрасываем, далее мы принудительно задаем вместо предельно уменьшившегося прироста угла его новое значение

ellipse

При такой замене замечаем, что уже на первых шагах угол α начинает резко возрастать. При этом круги полуосей и их эллипсы быстро "разбегаются". Но это происходит до некоторой максимальной величины прироста, после чего вновь наблюдается сближение эллипсов и кругов. При следующем совпадении эллипсов и кругов мы получаем базовый эллипс, полуоси которого равны полуосям целевого эллипса: b_AB = b_CD. При повороте базового эллипса CD0, он совпадает с целевым AB0, а точки C и D совпадают с точками A и B, соответственно. Угол поворота φ определяется уравнением (рис.2.6.9, рис.2.7) после окончательного слияния эллипсов C и D

Поворот базового эллипса или, что тождественно, построение целевого эллипса производим по уравнению (1.6). Можно сказать иначе: мы одновременно строим два эллипса CD0 и AB0. Для первого у нас есть главный, основной параметр - полуось b. Этот эллипс строим по параметрическим уравнениям (1.2)

Второй, целевой - по уравнениям (1.6) и известному, вычисленному углу φ. Для построения не всего целевого эллипса, а только дуги между точками A и B, находим параметрические углы этих точек ω_A = ω_C и ω_B = ω_D. Следовательно, на печать, на экран выводим только точки целевого эллипса из этого диапазона параметрических углов - рис.2.6.9 и рис.2.7. Подробнее этот процесс описан в следующем разделе. Задача решена: между произвольными точками A и B проведена геодезическая, дуга эллипса в круге Римана.

ellipse

Рис.2.7. Определение полярных углов, определяющих начало ω_D и конец ω_С дуги эллипса.

Проведение дуги эллипса от точки до точки

Приведённые выкладки являются решением сформулированной основной задачи: проведения полноразмерной геодезической на диске Римана через две произвольно заданные точки. Методика позволяет производить любые построения на диске с использованием геодезических, аналогов прямых линий Евклида.

Но, как отмечено, решение даёт полноразмерный эллипс, проходящий через две произвольные точки. Вместе с тем, более интересной и полезной является задача проведения отрезка такого эллипса, отрезка, находящегося точно между этими двумя точками. Для построения такого отрезка между точками нам нужно, по сути, лишь определить начальное и конечное значения полярного угла ω и строить эллипс только в этом диапазоне.

ellipse

Рис.2.8. Связь векторного α и полярного ω углов точки C

Эти полярные координаты, заметим, определить довольно просто. На рисунке видим, что полярный угол, например, точки C прямо зависит от соответствующей абсциссы этой точки

В свою очередь, абсцисса зависит от угла α этого вектора C. Используем принятые в нашей в работе обозначения

Сопоставляя эти два уравнения, находим

Откуда находим полярный угол

Это выражение учитывает углы с точностью до знака, определяющего квадрант нахождения полярного вектора и формируемой им точки эллипса, поскольку углы α и ω всегда находятся в одном квадранте. Полярная координата другой точки определяется таким же уравнением. Полярный угловой диапазон отрезка эллипса, таким образом, определяется системой уравнений

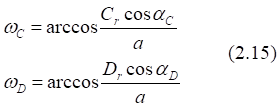
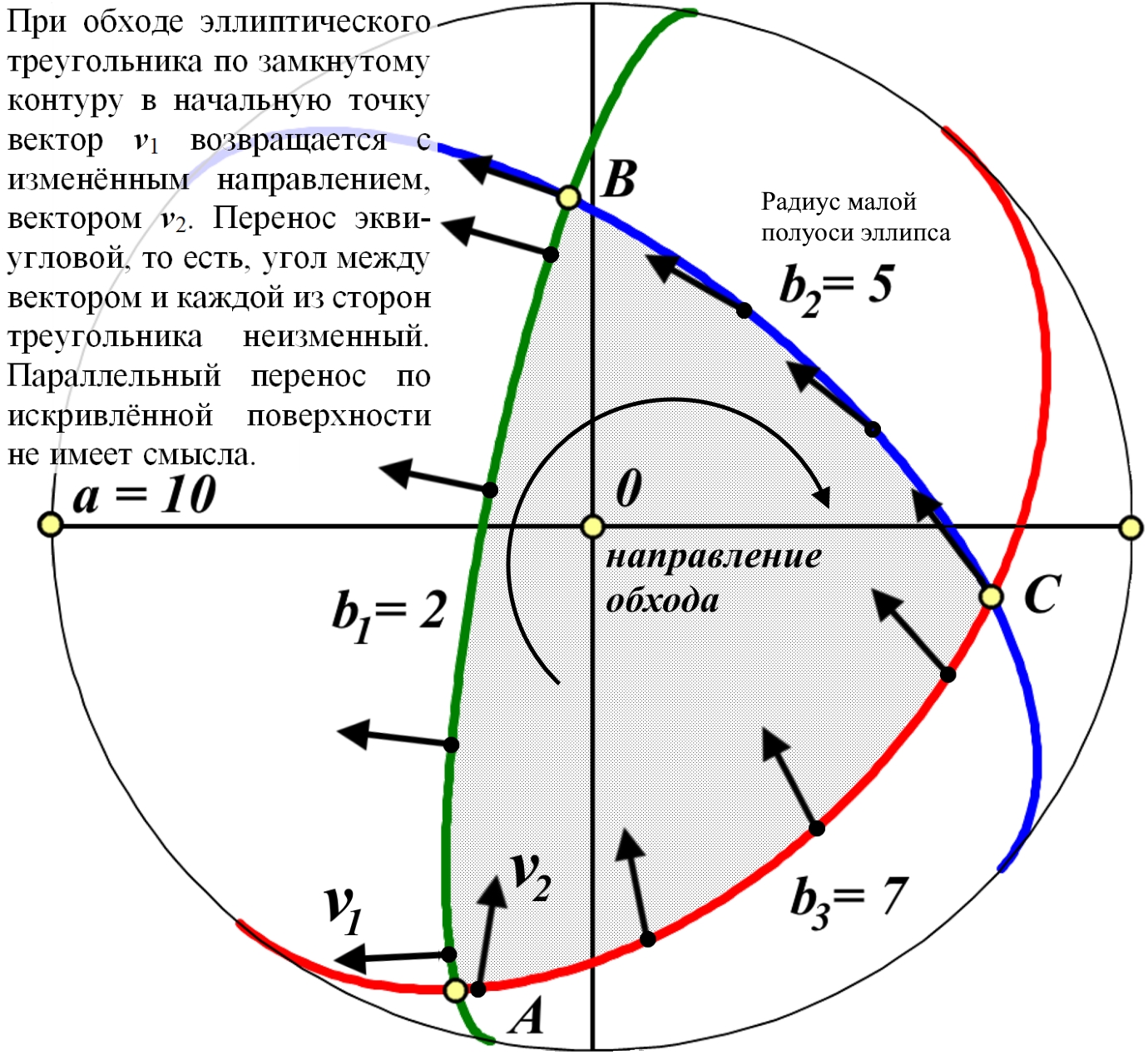
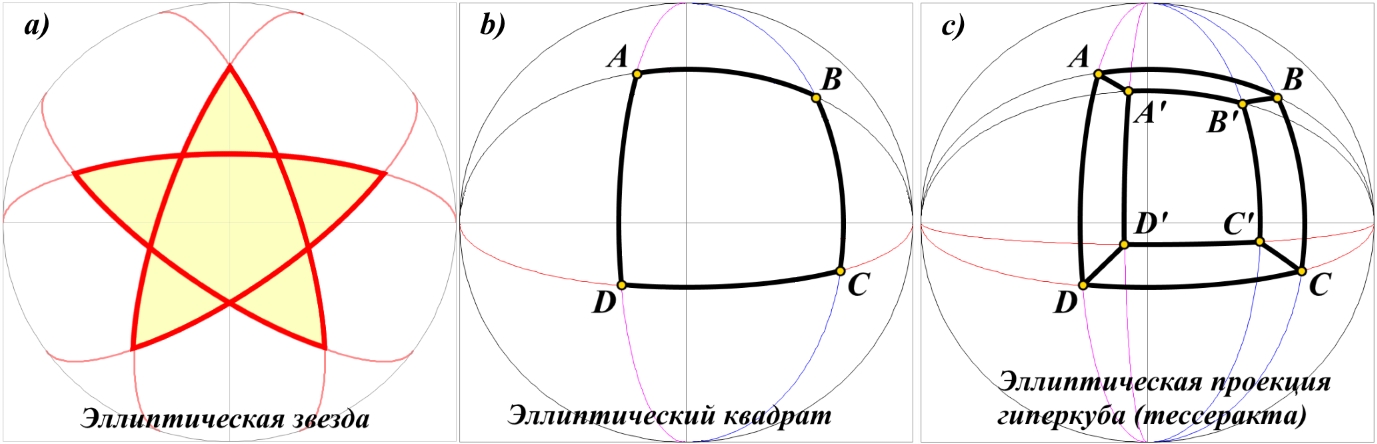
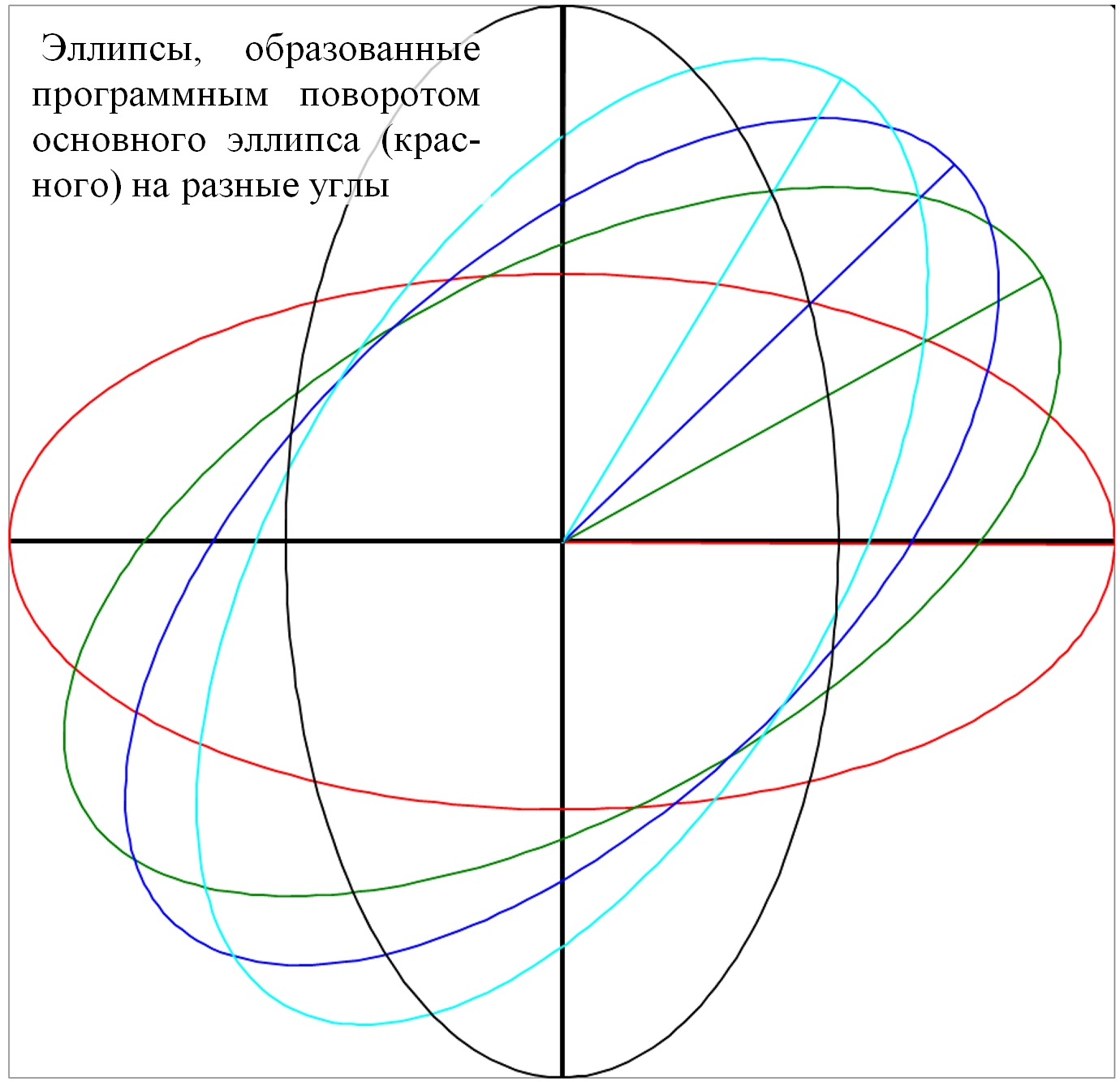
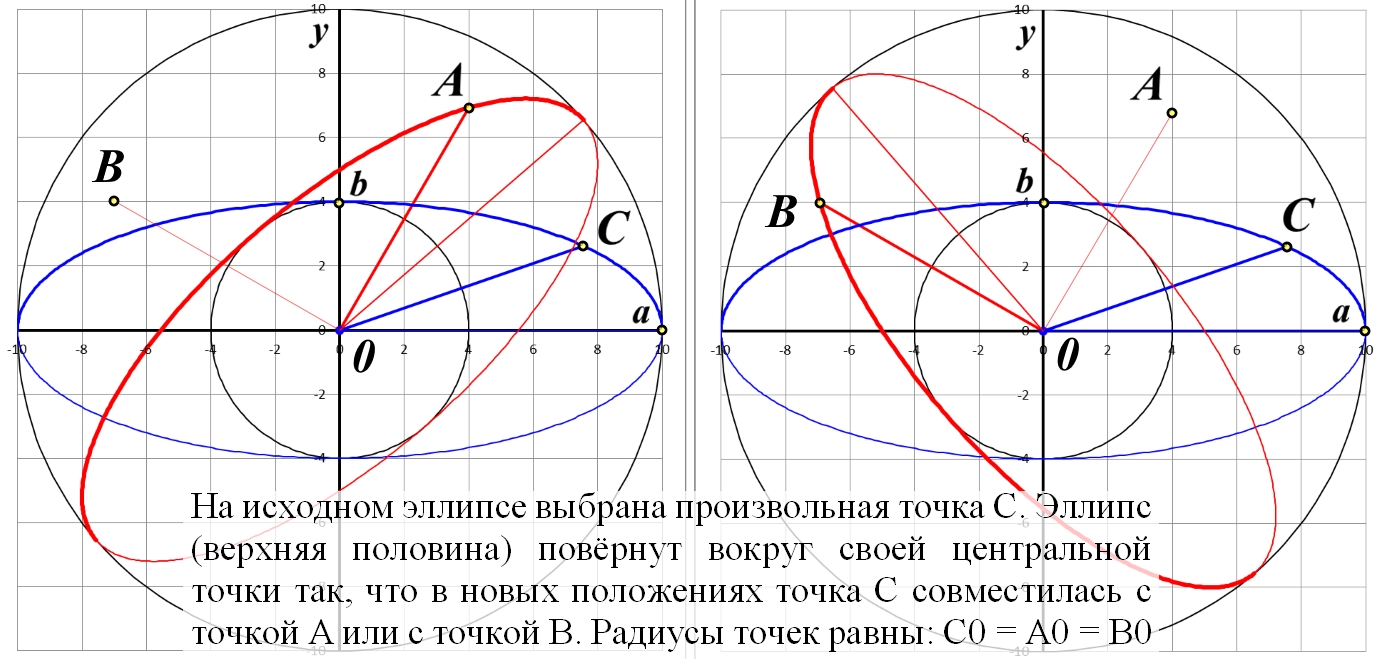
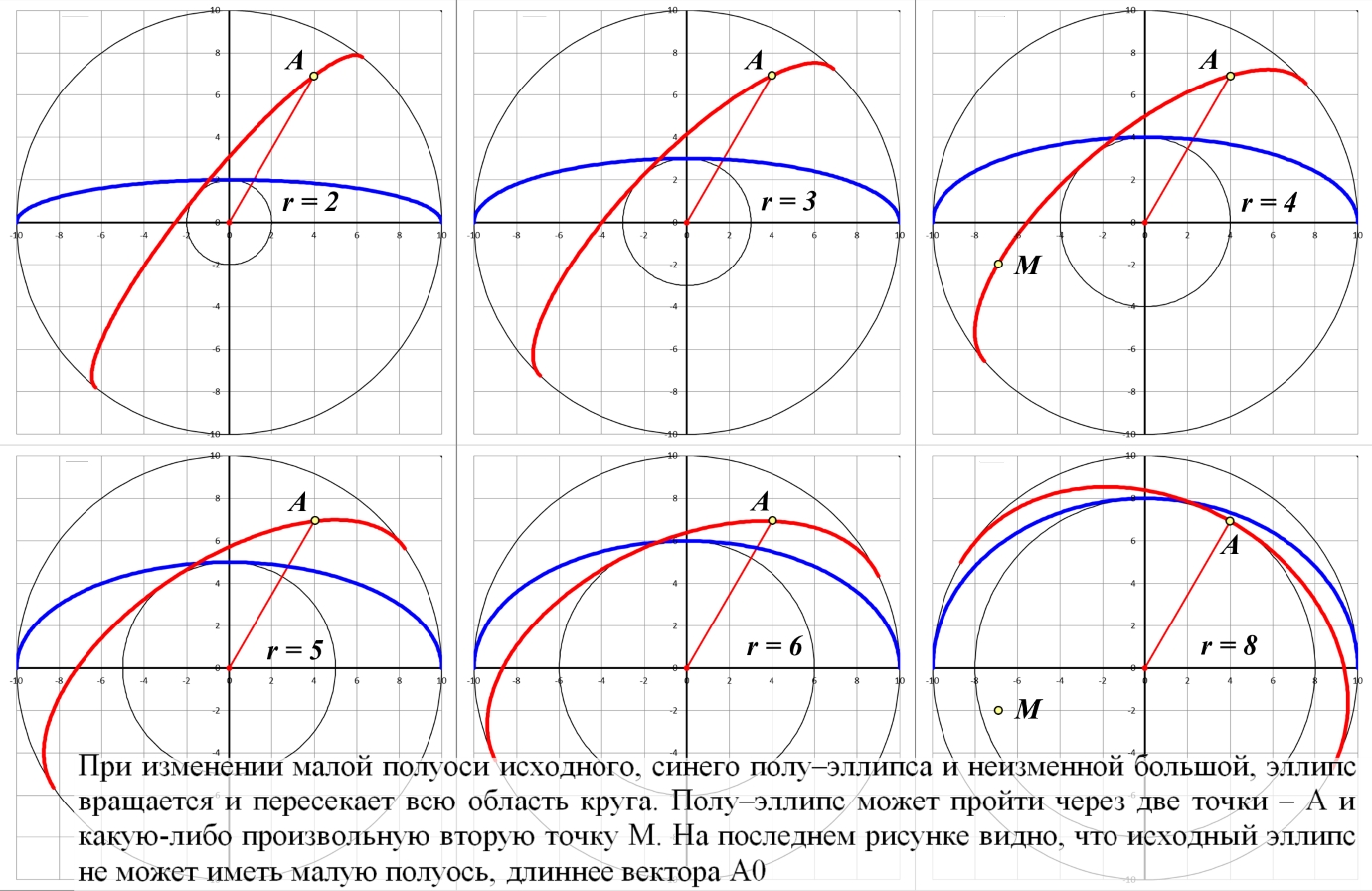
ellipse

Здесь величины Cr и Dr обозначают длины соответствующих векторов, векторные углы α которых обозначены как α_C и α_D. Построение базового эллипса перед его вращением производим от меньшего полярного угла ω_C до большего - ω_D.

3. Фигуры на диске Римана

Использование описанного алгоритма для построения отрезка эллипса на диске Римана позволяет строить на нём различные геометрические фигуры. Фигуры должны состоять из отрезков прямых линий диска Римана, геодезических, каковыми являются отрезки эллипса, в нашем случае, его верхней части.

Простейшей геометрической фигурой можно назвать треугольник. В криволинейных пространствах именно треугольник используется наиболее часто для демонстрации кривизны путём параллельного переноса вектора. В частности, при переносе вектора по поверхности сферы, он приходит в исходную точку с изменённым направлением. Диск Римана описывает точно такое же двухмерное пространство положительной кривизны. Рассмотрим, как изменится направление вектора при его эквиугловом переносе по замкнутой траектории, по сторонам треугольника на диске. Мы используем эквиугловой перенос, поскольку параллельный перенос в искривлённых пространствах не имеет смысла [3]. Эквиугловой означает перемещение с сохранением угла относительно линии переноса.

ellipse

Рис.3.1. Перенос вектора по сторонам эллиптического треугольника. Перенос эквиугловой, то есть, угол между вектором и каждой из сторон треугольника неизменный. Параллельный перенос по искривлённой поверхности не имеет смысла. Радиусы малых полуосей эллипса обозначены b₁...b₃

Как видно на рисунке, при обходе эллиптического треугольника по замкнутому контуру, в начальную, исходную точку вектор v₁ возвращается с изменённым направлением, векторомv₂. Для построения треугольника использованы эллипсы, имеющие длины малых полуосей b₁, b₂ и b₃.

Мы не рассматриваем простейшую фигуру - круг, поскольку он не может быть построен только геодезическими. Поэтому следующей по сложности простейшей фигурой можно считать четырёхугольник, в частности, квадрат рис.3.2b. На всех рисунках мы оставили тонкие контурные линии, полноразмерные геодезические, эллипсы, по которым построены соответствующие фигуры.

Пожалуй, предельно простой в построении эллиптической фигурой является пятиконечная звезда с центром в центре диска рис.3.2a. Образуется она простым вращением на 360:5 = 72 градуса пяти одинаковых дуг эллипса.

Отдельным интересным вариантом является квадратичная фигура - проекция гиперкуба на плоскость рис.3.2c. Заметим, что примерно так же будет выглядеть и эллиптическая аксонометрия обычного куба.

ellipse

Рис.3.2. Эллиптические фигуры на диске Римана

Завершающая процедура построения фигур - построение по точкам. Разработан алгоритм, позволяющий строить фигуры простым последовательным перебором точек. Отрезки эллипсов проводим от некоторой текущей точки к следующей за ней. Этот способ позволяет построить практически любую фигуру, состоящую из последовательности отрезков.

4. Сфера (шар) Римана

Ранее, рассматривая диск Пуанкаре как симуляцию двухмерного пространства отрицательной кривизны Лобачевского, мы предложили также и трёхмерную симуляцию пространства Лобачевского [5], назвав её сферой Лобачевского. В данной работе мы также можем перейти от двухмерного пространства на диске Римана к трёхмерному эллиптическому пространству, симуляцию которого назовём трёхмерной сферой, шаром Римана.

Рассмотрим различия и терминологическое сходство координатных понятий на традиционной двухмерной сфере и в трёхмерном шаре Римана. На сфере, как известно, геодезическими являются наикратчайшие линии, подчеркнём - линии. Такими линиями являются большие круги сферы. В шаре Римана, как и в сфере Лобачевского, появляется новое понятие геодезической - это геодезическая двухмерная поверхность, в качестве которой мы выбрали верхнюю часть эллипсоида (сфероида). У геодезических линий есть определяющее свойство - это наикратчайшая линия между двумя точками. Такое же минималистическое свойство можно обнаружить и у геодезических поверхностей: это поверхность минимальной площади, наименьшая площадь некоторого замкнутого контура, своеобразный эквивалент плоскости в пространстве Евклида.

Можно предположить, что "геодезическая" последовательность: линия - поверхность имеет продолжение. Линия принадлежит двухмерному пространству, поверхность - трёхмерному. Следовательно, что-то должно принадлежать, скажем, четырёхмерному пространству. Если рассмотреть способ перехода от линии к поверхности, то можно обнаружить их явную интегральную связь. Более того, первичным объектом в этой связке является точка. Первый интеграл по точке даёт нам линию. Второй интеграл по точке или первый интеграл по линии даёт уже поверхность. Интеграл по поверхности, очевидно, даёт нам объём. Получается, что следующей геодезической величиной следует считать некий геодезический объём. Видимо, следует считать, что такая геодезическая также обладает неким минималистическим свойством. Закономерно предположить, что это минимальный объём некоторого четырёхмерного объекта, хотя осознать смысл этого непросто. Если продолжить последовательность, то следующую геодезическую можно найти как результат очередного интегрирования. Как правило, четвертый интеграл уже не имеет явно выраженного пространственного свойства. В ряду точка - линия - поверхность - объём этот интеграл явно имеет свойство массы. Следовательно, очередная геодезическая - это минимальная масса. Следует признать, что этот вариант выглядит ещё более абстрактно, хотя и довольно последовательно вписывается в рассмотренный ряд.

Часто используемым свойством геодезических линий является изменение направления вектора при эквиугловом перемещении по замкнутому контуру вдоль них. Закономерно возникает вопрос, а есть ли подобное "перемещение", некий его аналог у других видов геодезических? Изменение направления вектора рассматривается как свидетельство кривизны этого двухмерного пространства. А что можно переместить по геодезической поверхности? Можно предположить, что замкнутый контур из таких геодезических представляет собой просто некое тело в искривлённом трёхмерном пространстве. В двухмерном искривлённом пространстве вдоль геодезической линии перемещается тоже линия, вектор, причём с сохранением угла по отношению к линии переноса. В трёхмерном же искривлённом пространстве подобное относительное перемещение представить довольно трудно. Даже само понятие перемещения в этом случае вызывает массу вопросов. Ещё более сложной является ситуация с четырёхмерными объектами.

Но вернёмся к эллиптическому пространству. Все рассматриваемые эллиптические геодезические поверхности имеют две одинаковые оси, равные диаметру шара (сферы) Римана. Третья, переменная ось сфероида играет роль третьей координаты в шаре Римана.

На рисунке рис.4.1 приведены сфероид и раздельно его верхняя и нижняя части. Такое разделение мы выбрали по тем же основаниям, что и верхнюю часть эллипса на диске Римана. Через любые три точки в шаре можно провести два разных эллипсоида, касающиеся этих точек либо только одной, либо двумя поверхностями. Это утверждение мы приводим без доказательств, опираясь умозрительно на такое же свойство эллипса.

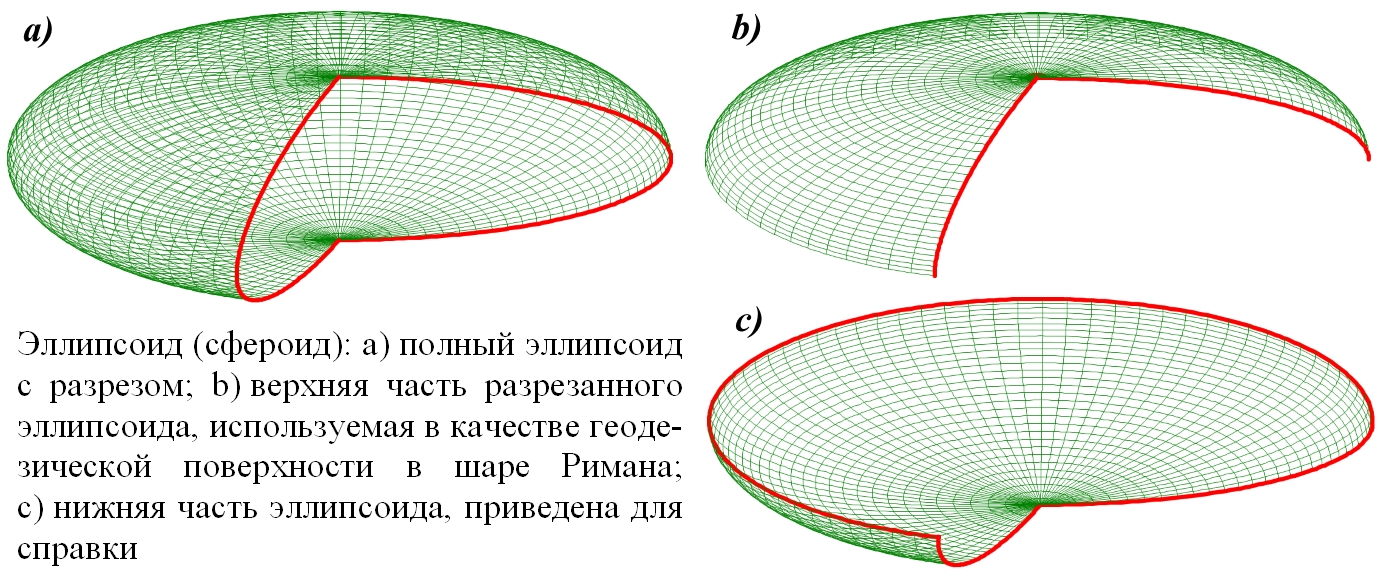
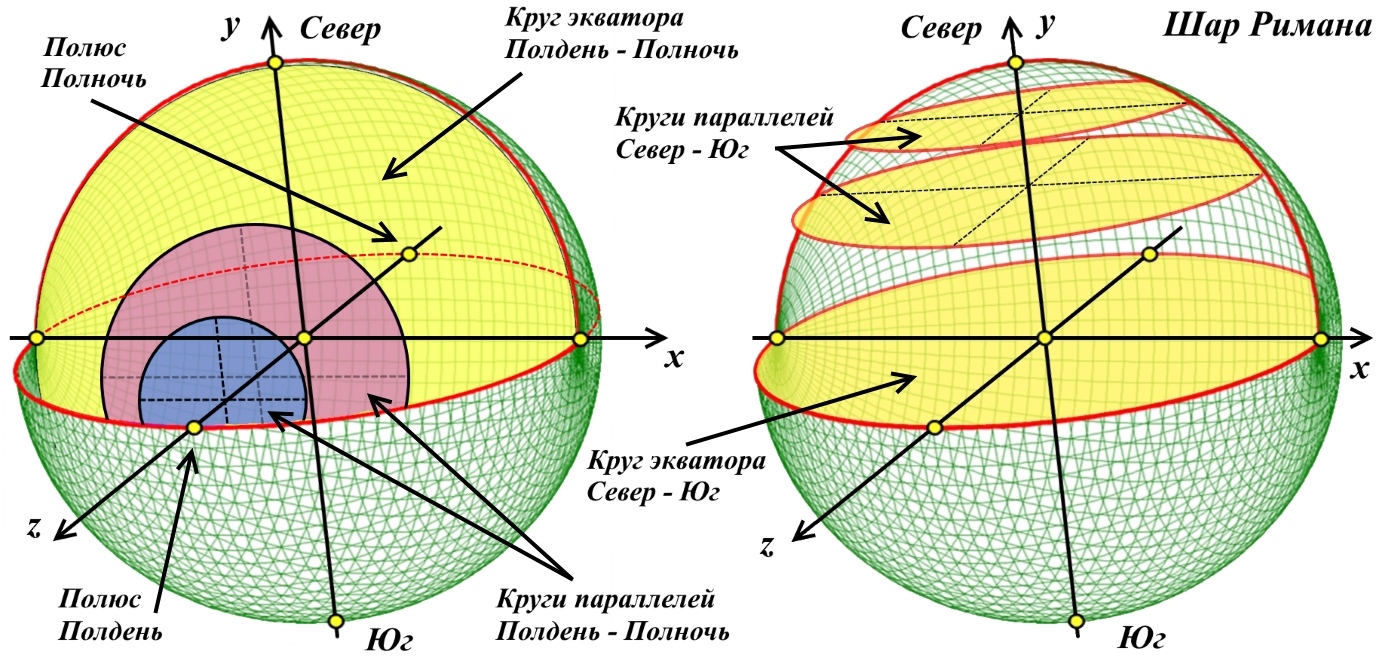
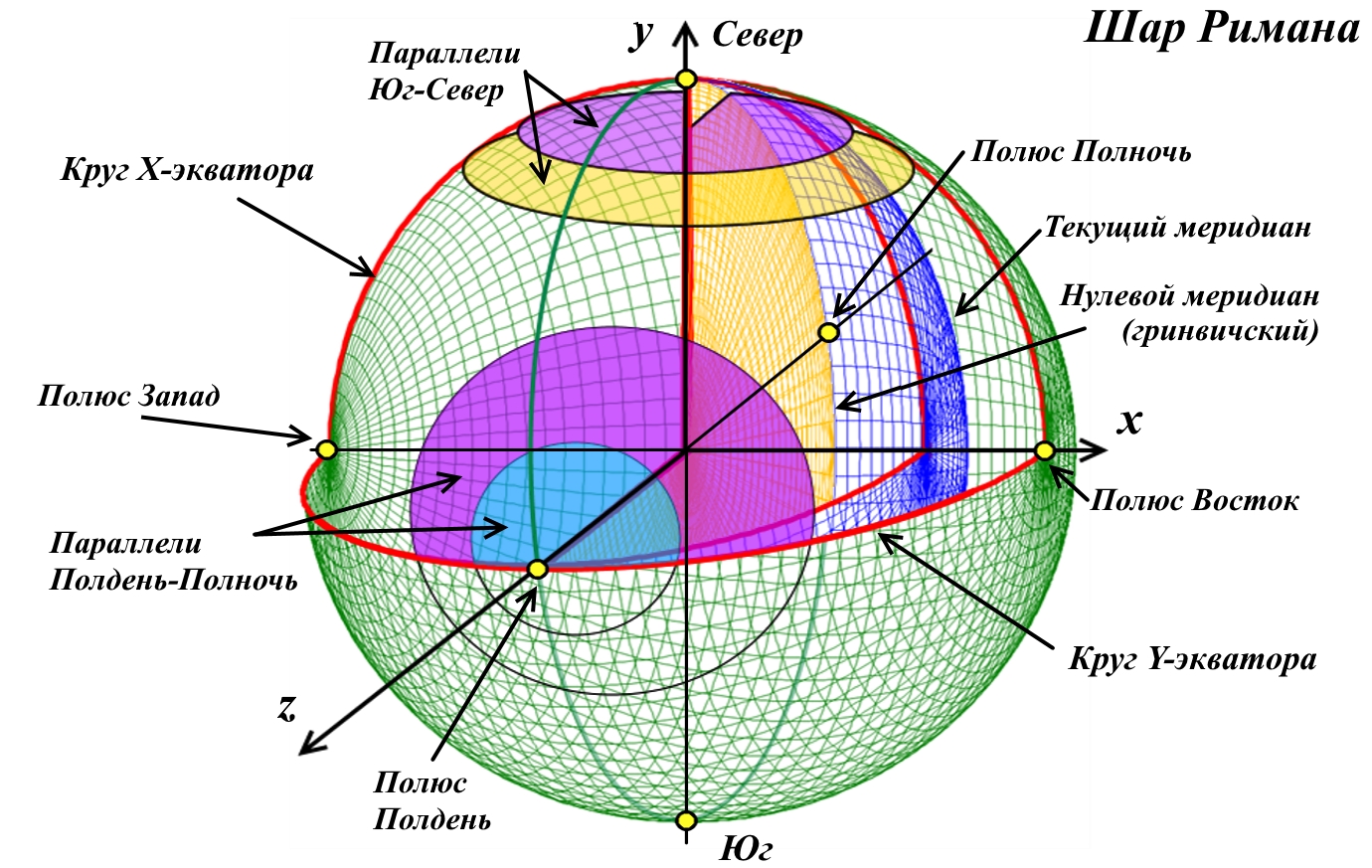
ellipse

Рис.4.1. Эллипсоид (сфероид) как геодезическая поверхность: a) полный эллипсоид с разрезом; b) верхняя часть разрезанного эллипсоида, используемая в качестве геодезической поверхности в шаре Римана; c) нижняя часть эллипсоида, приведена для справки

За основу системы координат шара возьмём традиционную меридианную систему. Третьей, дополнительной пространственной координатой в шаре будет эллипсоид, третья ось которого, не равная другим, является переменной. Нулевое значение этой оси создаёт начальную точку этой меридианной координаты, нулевой пространственный меридиан. Понятно, что он имеет форму круга. Окружность этого круга является эквивалентом полюсов на сфере: каждая из сторон этого круга тождественна южному или северному полюсу сферы.

Параллелями являются круги, ортогональные к двум другим координатам - Y и Z. Из этого становится очевидным, что сфера, шар Римана имеет два пространственных экватора - это самые большие ортогональные круги. Наибольшее и наименьшее значения оси X можно назвать, соответственно, западом и востоком шара Римана. Понятно, что экваториальные бесконечно тонкие эллипсоиды шара, экваторы являются двумя единственными плоскими параллелями, пространственными геодезическими шара Римана. На сфере такой единственной "прямой" параллелью, геодезической линией является экватор.

ellipse

Рис.4.2. Координатная система шара Римана в терминах меридианов и параллелей

Координаты любой точки в шаре Римана формируются пересечением трёх поверхностей. Два диска параллелей, на которых находится точка, при пересечении образуют линию, параллельную оси X. Эта линия неизбежно пересекает и меридиан, на котором оказывается эта точка. Обозначение координат точек с использованием меридиан и параллелей имеет специфическую особенность: координаты не зависят от физических размеров объекта, сферы. Пример: пусть в шаре Римана диаметром 10 (метров, километров, световых лет) задана точка с декартовыми координатами М(x = 3, y = 5, z = -7). Пересчитаем эти координаты в полярные, меридианы и параллели. Круг y-параллели Север-Юг удалён от своего экватора на полярный угол, равный

Другой круг, круг z-параллели Полночь-Полдень, виден под своим полярным углом

Иначе определяется меридиан между полюсами Запад-Восток. Точка лежит на поверхности сфероида, описываемого в наших обозначениях каноническим уравнением, из которого после преобразований находим декартову величину меридиана m, которую затем преобразуем в линейную угловую

ellipse

Линейная угловая величина на самом деле углом как таковым не является, это величина, записываемая как угол, в градусах. Например, если обозначить высоту трёхэтажного дома как 2π некоторых условных "метров", то высота первого этажа будет, очевидно, равна ~ 2 условным метрам или 120 градусам. Полное обозначение координат рассмотренной точки М будет звучать следующим образом: 17 градусов 28 минут северной широты, 44 градуса 26 минут полуденной широты и 105 градусов 54 минуты западной долготы [4, с.152].

Отметим, что мы использовали традиционный диапазон изменения меридианов: от - 180 до + 180 градусов. Можно сказать, что мы приносим математическую необходимость в жертву традициям. Сфера Римана при таком угловом диапазоне превращается в угловой эллипсоид. Действительно, по двум другим осям угловые диапазоны равны точно 180 градусам, а по меридианной оси, как видим, диапазон равен 360 градусам.

В отличие от шара Римана, запись координат на Земле имеет только два параметра, то есть, формально координаты описывают двухмерное пространство. Неявно третьей пространственной координатой в этом случае является так называемая "высота над уровнем моря". В космическую эру она продлена на околоземное пространство. Заметим, что в шаре Римана возможны ещё три принципиально различающиеся формулы координат: широта - широта - широта, широта - долгота - долгота и долгота - долгота - долгота. Однако дополнительный меридиан, долгота в обозначении фактически предполагает наличие реальных дополнительных геометрических полюсов, таких, что, находясь на одном из них, по всем направлениям будет виден только парный ему полюс. Например, на Земле, на южном или северном полюсах отсутствует понятие Запад-Восток, все направления указывать на парный полюс.

В отличие от земных географических координат, шаровые координаты образуются не линиями меридианов и параллелей, а поверхностями сфероидных меридианов и дисков параллелей. На Земле самая большая параллель является экватором. Следовательно, в шаре Римана такими же экваторами являются также самые большие параллели, причём экваторов в шаре два - самые большие круги, ортогональные осям Z и Y. Соответственно, нулевым, гринвичским меридианом является такой же круг, проходящий через обе декартовы координатные оси Z и Y. Следует признать, что рисунок рис.4.2 чрезмерно загружен деталями и просматривается не очень хорошо. Поэтому приведём его в "разобранном" виде.

ellipse

Рис.4.3. Система координат шара Римана. Слева параллели и экватор оси Z; справа параллели и экватор оси Y

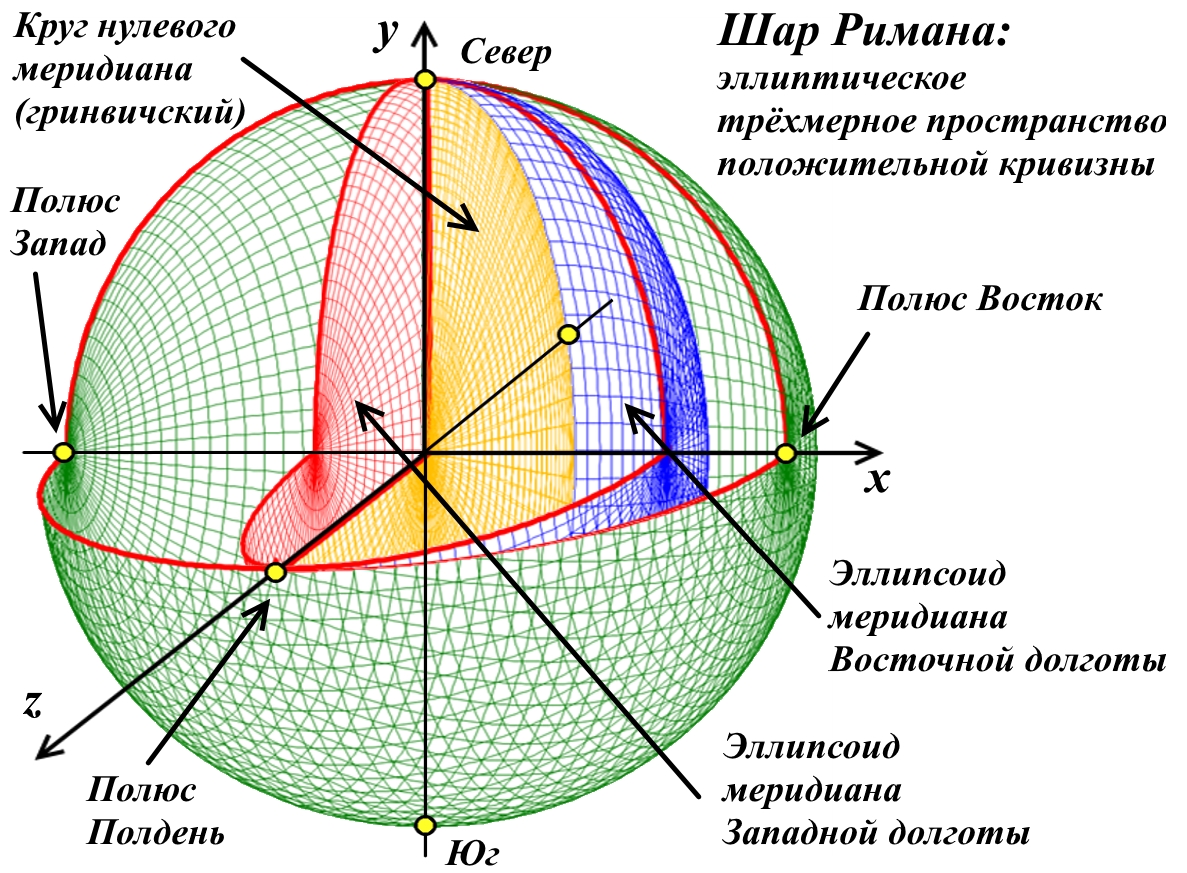
ellipse

Рис.4.4. Система координат шара Римана: меридианы.

Введение понятия геодезической поверхности предполагает, что такая поверхность должна быть однозначно определена для некоторых особых случаев, то есть, должна быть единственной. Таким особым случаем, очевидно, должно быть такое же условие, как и на диске-симуляции двухмерного эллиптического пространства положительной кривизны. Это условие гласит, что через три точки в сфере Римана проходит единственный эллипсоид, сфероид.

По сравнению с диском Римана в данном случае вместе с увеличение числа координат, увеличивается также и число точек, определяющих геодезическую. В сущности, это очевидное обстоятельство. Известно подобное правило для сферы: через три произвольные точки можно провести две сферы заданного радиуса. Мы используем "сжатые" сферы - сфероиды, одну из половин которых отбрасываем. Следовательно, вместо двух полных сфероидов у нас остаётся только один полу-сфероид. Действительно, "нижний" сфероид проходит через точки своей верхней поверхностью, нижняя отброшена. Верхний же должен пройти через точки своей нижней поверхностью, но её мы отбрасываем, отбрасывая тем самым и весь сфероид.

Исходя из этого, ставится задача построения такого сфероида для произвольно заданных трёх точек. Пусть это будут точки A, B и С. Исходя из проведённых исследований с эллипсами, очевидно, что и в этом случае задачу можно разбить на два этапа. Первый этап, это на основе полученных для эллипсов решений следует провести произвольный, базовый эллипсоид через две заданные точки. Решение предполагает построение по двум точкам, радиус-векторам некоего эллипса, который является сечением этого базового эллипсоида. Такое решение возможно, поскольку ортогональные сечения сфероида являются эллипсами. Далее необходимо повернуть этот базовый эллипсоид вокруг большой оси построенного эллипса до пересечения его поверхности с третьей точкой. Очевидно, что и это решение является единственным, поскольку эллипсоид при вращении своей поверхностью пересекает, "заметает" весь внутренний объём шара.

На рисунке рис.4.5 изображена обобщённая картина вращения точек и построенного на них сфероида. Поверхность шара Римана не показана, она подразумевается. Сфероид, полу-эллипсоид зелёного цвета - это поверхность, построенная на эллипсе, проведённом через повернутые в новую плоскость x'0y' точки A и B. Этот сфероид "ожидает" последней процедуры - вращения вокруг большой оси эллипса до совмещения с точкой C. Угол вращения определяется так же, как и в задаче с эллипсами. Для этого проводятся две секущие плоскости - круги P и S. Круг P проводим через ось Y и конечную точку C, а круг S - через точку C ортогонально оси X. Этот круг пересекает построенный эллипсоид в точке D, радиус-вектор которой должен быть равен радиус-вектору точки C. Мы используем термин радиус-вектор, просто чтобы подчеркнуть, что его начальная точка лежит на какой-либо оси, вокруг которой предполагается вращение объектов, связанных с этим вектором. Все линии пересечения однозначны и позволяют определить как декартовы координаты точки C, так и углы радиус-векторов C и D, фактически угол предстоящего вращения эллипсоида.

Действительно, использованные секущие круги однозначно определяют декартовы координаты точки C - С_x, C_y и C_z, а, следовательно, и угол наклона радиус-вектора C0 в плоскости круга S. Точка D лежит на линии эллипса, образованного при сечении базового эллипсоида ортогональной плоскостью. Поскольку известен его радиус-вектора и, фактически, малая полуось этого эллипса, мы можем найти и угол этого радиус-вектора в плоскости круга S.

Далее поворачиваем эллипсоид на угол между точками C и D, в результате чего точка D на эллипсоиде, сфероиде совместится с точкой C. Это является решением задачи в повёрнутой системе координат x'y'z': теперь все три точки A, B и C лежат на поверхности одного сфероида.

ellipse

Рис.4.5. Построение сфероида (эллипсоида), проходящего через три заданные точки - A, B и C. Точка D на поверхности эллипсоида (сфероида) - это точка, которая при его вращении совместится с точкой C внутри сферы Римана.

Новые координаты

Рассмотрим описанные преобразования подробнее, по шагам, используя "проволочные" рисунки вместо объёмных, аксонометрических. Все построения мы производим в новой, повёрнутой системе координат, что позволяет использовать полученные выше результаты с вращением эллипсов. В этой системе оси базового эллипса совпадают с осями координат.

Переход в такую новую, удобную систему координат можно произвести разными способами. Один из них - традиционный, математический. Сначала производим вращение пирамиды ABC0 вокруг некоторой оси таким образом, что плоскость грани AB0 расположилась горизонтально. Для этого, очевидно, нам нужно найти угол φ_N между исходной плоскостью x0y и плоскостью после поворота. Ясно, что этот угол равен углу между осью z0 и некоторым вектором N₁, ортогональным к плоскости грани AB0. Удобно взять такой вектор также в виде радиус-вектора, начинающегося в общей нулевой точке обеих систем координат. Этот ортогональный вектор N₁(x, y, z) мы можем найти путём векторного произведения двух векторов A_r и B_r.

ellipse

Рис.4.6. Последовательными векторными произведениями построены вектор N₁ и вектор N₂, который лежит в плоскости грани AB0. Вектора N₁ и N₂естественным образом "назна-чаются" координатными осями z' и x'

Точные значения и детальные уравнения нас не интересуют, поэтому просто приведём выражение, определяющее этот угол. Вычислив векторное произведение, находим вектор, нормальный к плоскости грани AB0. Угол между двумя плоскостями - xyz и плоскостью грани равен углу между вычисленным вектором и осью z0.

ellipse

Для собственно поворота грани нам необходимо вычислить ещё одно векторное произведение, найти некий вектор N₂, ортогональный к плоскости векторов N₁ и z0. Понятно, что эта ортогональность вектора N₁ превращает его в одну из координатных осей новой системы координат. Поскольку вектор N₁ мы определённо назначим остью z'0, другой новый вектор N₂, соответственно, может быть назначен осью x'0. Длину вектора для вычисления примем равной единице

ellipse

Оба вычисления мы производим в исходной системе координат xyz, поэтому все проекции векторов также относятся к ней. Итог вычислений состоит в том, что три вектора N₂, A_r и B_r лежат в одной плоскости. В этой плоскости, образующей новую систему координат x'y'z', координаты векторов A_r и B_r будут иными, причём z-координаты этих векторов будут равны нулю. Заметим, что вектор, линия N₂ - это линия пересечения двух плоскостей - исходной x0y и плоскости грани AB0.

В соответствии с изложенными правилами вращения плоскости, мы определяем, что вектор N₂ ортогонален к оси z0. Следовательно, он лежит в плоскости x0y. Координаты этого вектора нам известны по вычислениям, поэтому также известен и угол между N₂ и осью x0. Обозначим этот известный нам угол символом ψ. Но кроме этого, этот же вектор N₂ по определению лежит и в плоскости грани AB0. Прямая линия, вектор N₂, перпендикулярный к вектору N₁, который перпендикулярен к плоскости AB0, лежит в этой плоскости. Описанные характеристики векторов N₁ и N₂ явно соответствуют их ролям, как осей новой системы координат: z' и x'.

Однако следует отметить: данный способ перехода в новые координаты нам не подходит. При всей его математической состоятельности, он не позволяет построить базовый эллипс с координатными осями. Требуется дополнительная операция - поворот новых осей координат таким образом, чтобы оси базового эллипса AB0 совпали с этими осями координат.

Автоматические новые координаты

Переход к новым координатам можно произвести иначе. Явочным, принудительным порядком устанавливаем, что треугольник AB0 лежит в координатной плоскости x'0y'. Далее строим на этой плоскости эллипс с центром в начале координат и проходящий через точки A и B. Используем уравнения (2.2), (2.3) и (2.4), переписав их в текущих обозначениях

ellipse

Решение, как мы выше показали, единственное. При этом автоматически образуется собственная координатная система, плоскость эллипса, наклонённая к исходной координатной плоскости x0y под некоторым, неизвестным нам углом. Все точки - A, B и C в новой повёрнутой системе координат x'y'z' получают новые координаты, причём координаты z точек A и B становятся равными нулю. Длины векторов A0, B0 и C0 при этом остались неизменными. Соответственно, неизменной осталась и исходная пирамида ABC0. Следовательно, координата z точки C в новой, повёрнутой системе координат x'0y' стала равной высоте пирамиды над плоскостью грани AB0. Построенный эллипс AB0 является базовым эллипсом, рассмотренным в предыдущих разделах.

ellipse

Рис.4.7. Явочным порядком плоскость грани AB0 "уложена" на плоскость x0y новой системы координат. В качестве осей x' и y' в этой системе координат "наз-начены" полуоси эллипса AB0, проведённого через точки A и B.

Заметим, что в новой системе координат угол между векторами A0 и B0 не изменился, поэтому принимаем без вычислений его прежнее значение - угол γ. Все вычисления в предыдущих разделах мы производили с осью x, в роли которой выступала большая полуось эллипса AB0. Здесь эта ось просто переименована в x'. Поэтому вычисления новых координат векторов A, B и C мы будет производить относительно этой оси, угол α которой мы вычислили ранее (1.13), исходя из свойств эллипса AB0. Другими словами, осью x'0 мы назначаем не вектор N₂, имеющий на это полное право, а более удобную для вычислений большую полуось эллипса AB0.

Координаты точки C

После перехода к новым автоматическим координатам необходимо определить новые координаты точки C. Заметим, что x' и y' координаты точек A и B мы определили в процессе построения эллипса. На следующем рисунке три рассматриваемые произвольные точки в шаре Римана вместе с его центром образуют треугольную пирамиду, в нашем случае пирамиду ABC0.

ellipse

Рис.4.8. Построение эллипса по радиус-векторам A0 и B0 в плоскости грани AB0, образующей систему координат x'y'z'

Для определения угла поворота переменной оси эллипсоида b'0 с целью совмещения его поверхности с точкой C, нам необходимо определить расстояние от начала координат ортогональной оси x'0 плоскости, в которой лежит точка C, то есть, величину C_x'. Именно в этой плоскости, сечении эллипсоида, сфероида находится радиус-вектор Dr = Cr некоторой точки D, которая при вращении совместится с точкой C. Такое совмещение и означает, что точка C будет лежать на поверхности повёрнутого базового сфероида, изначально построенного на полу-эллипсе, описанном вокруг треугольника AB0. Далее эллипс треугольника AB0 для краткости мы будем называть просто эллипсом AB0. Для лучшего восприятия на рисунке этот образующий, базовый эллипс AB0 изображён полностью, хотя в исследованиях мы принимаем во внимание только его половину, верхнюю часть, содержащую точки A и B.

Эллипс является центральным сечением искомого базового эллипсоида в повёрнутой системе координат. Сечение лежит в плоскости одной из двух главных, равных осей эллипсоида и в плоскости его меньшей, оси переменной длины. Из главных осей можно выбрать любую, в данном случае выбрана ось x', что соответствует ранее использованным обозначениям исследованных эллипсов.

Для определения угла поворота базового эллипса AB0 с его деформацией необходимо в первую очередь определить удалённость целевой точки C от плоскости y'0z'. Штрихи в обозначении осей означают их отношение к повернутой системе координат, плоскости треугольника AB0. Направление осей при этом задают оси построенного на треугольнике эллипса AB0. Рассмотрим рисунок рис.4.8 с другой точки, с другого направления - со стороны положительного направления оси z', то есть, будем смотреть сверху на плоскость треугольника AB0, рис.4.9. Последовательно определим величины, уже известные по условиям задачи, и величины, которые можно вычислить с их использованием. Вид А рассмотрен на рисунке рис.4.11.

ellipse

Рис.4.9. Шар Римана. Определение координат целевой точки C, которой при вращении коснётся эллипсоид, построенный на эллипсе AB0

Известные основные величины - это длины рёбер пирамиды ABC0, которые обозначим как R_AB, R_AC, R_A0 и так далее, где индексы означают начальную и конечную точку соответствующего ребра. Можно использовать и тождественное, векторное обозначение рёбер, начинающихся в начале координат: A_r, B_r и C_r, либо R_A, R_B, R_C. Производные, вычислимые параметры системы - это углы между рёбрами, которые можно определить по стандартным соотношениям в соответствующих треугольниках. Еще двумя важными для вычислений величинами являются длина малой полуоси эллипса AB0 и зависимый от неё фокус эллипса.

Интересующее нас удаление C_x' точки C от плоскости y'0z', как видно на рисунке рис.4.9, равно

где отрезок C_x'y' - это проекция ребра R_C0 на плоскость x'0y'. Длину этого отрезка мы можем определить из выражения

Отрезок C_z' - это высота пирамиды над плоскостью её грани AB0. Величина эта определяется стандартными уравнениями для пирамиды, поэтому мы просто обозначим её как известную. Следовательно, и величину C_x'y' мы также принимаем как известную, поэтому

Для определения этой удалённости теперь нам необходим угол δ. Этот угол, согласно рисунку, определяется из соотношения

Второй из углов справа в уравнении, ω₂ определяем, используя свойства построенного эллипса AB0:

Здесь все углы справа мы считаем известными. Первый угол, ω₁ определяется из соотношения сторон треугольника B0C_x'y', которые известны, поскольку известны координаты вершин треугольника в плоскости x'0y'. Действительно, нижнюю сторону треугольника C_x'y' мы уже определили. Левая его сторона определяется аналогично

Второй справа угол в уравнении для ω₂, угол γ определяется из соотношений треугольника AB0, а третий - α, однозначно определяется свойствами построенного эллипса, как выше мы уже показали. Действительно, рассмотрим вновь уравнения (2.2) и (2.3), переписав их под текущие обозначения

ellipse

Напомним, что все рассматриваемые величины имеют координаты в штриховой системе координат x'y'z'. Преобразуем уравнения

Также перепишем уравнение (2.7) в текущих обозначениях

Таким образом, мы получили два уравнения с двумя неизвестными - A_x' и B_x'

ellipse

Используя разработанный выше итерационный метод, вычисляем проекции векторов A_x' и B_x', после чего находим фокус и полуоси a, b = b' эллипса AB0, а также искомый начальный угол α вектора A0. Таким образом, искомый угол δ проекции 0С_x'y' вектора C0 с осью x'0 и отрезок C_x', согласно уравнению (4.1), определяются известными величинами

ellipse

Ещё одной величиной, необходимой для дальнейших рассуждений, является длина радиус-вектора, соединяющего точку C_x' с точкой D на эллипсе AB0, имеющей такую же абсциссу - C_x'. Именно эта точка D при вращении радиус вектора С_x'D вокруг большой оси эллипса, оси x'0 и совместится с целевой точкой C. Длину этого радиус-вектора определяем из канонического уравнения эллипса AB0

ellipse

Пока мы рассматриваем некие абстрактные промежуточные объекты - точки эллипса. Однако все эти точки имеют самое непосредственное отношение к основному объекту - эллипсоиду, сфероиду, построенному в свою очередь на эллипсе AB0. Вращение эллипсоида на самом деле является несколько условным, поскольку при таком вращении эллипсоид, сфероид всегда проходит через базовый эллипс AB0. То есть, это вращение с деформацией. При этом радиус-вектор точки D на эллипсоиде сам не меняется, а лишь меняет радиальную точку своего нахождения на эллипсоиде.

Перед продолжением рассуждений сделаем полезное пояснение. На поясняющих рисунках рис.4.9 мы вновь изменяем направление взгляда: теперь мы рассматриваем систему со стороны положительного направления оси x', то есть, смотрим на плоскость y'0z', как показано стрелкой с надписью Вид A. Вращаемый эллипсоид мы видим теперь в виде набора его сечений, ортогональных оси x'0.

При вращении с деформацией эллипсоид, сфероид своей поверхностью "заметает" всю внутреннюю область шара. Покажем это на отдельном сечении сфероида - некотором эллипсе. Это может быть как центральное сечение сфероида, проходящее через центр сферы, так и любое параллельное ему. На следующих рисунках показаны несколько таких вращаемых эллипсов. На рисунке рис.4.10a эллипсы показаны с шагом в 1 градус, поэтому изменение их малой полуоси не заметно. На рисунке рис.4.10б шаг вращения увеличен до 15 градусов, поэтому теперь уже заметно, что крайние эллипсы имеют разные малые полуоси.

ellipse

Рис.4.10. Через заданную точку А проведены эллипсы. Слева угловой шаг равен 1 градусу; справа - 15 градусов. При вращении эллипсов меняется их малая полуось.

Изменение длины малой полуоси b вызвано изменением фокусов F при повороте эллипса, что в свою очередь связано с тем, что изменяется наклон базового вектора к большой полуоси, угол ψ, приводящий к изменению его проекции A_x' на эту ось. Отметим, что на рис.4.10 этот угол ψ для каждого из повёрнутых эллипсов - собственный и образован радиус-вектором A0 и большой осью этого эллипса. Изображённый на рисунке угол относится к базовому эллипсу, ось которого совпадает с горизонтальной осью.

ellipse

Преобразуем совместно эти уравнения

Проверим корректность уравнения по двум крайним, предельным значениям угла. Если ψ = 0, то полуось должна быть равна нулю b = 0. Это выполняется. Если угол ψ = 90 градусов, то полуось должна быть равна радиус-вектору R_A

И это условие выполняется. Уравнение можно считать корректным. Большая полуось у всех эллипсов одна и та же, равная радиусу шара Римана. Главное условие - прохождение всех эллипсов при вращении через одну и ту же базовую точку A, вектор которой изображён красным. Нетрудно догадаться, что при полном обороте эллипса его дуга "заметёт" всю поверхность круга. Следовательно, дуга вращающегося с деформацией эллипса обязательно коснётся любой точки в круге.

Далее рассмотрим рисунок, вид А на рисунке рис.4.9, демонстрирующий реальный процесс описываемого вращения. Заметим, что плоскость треугольника, эллипса AB0 на рисунке рис.4.11 выродилась в линию AB0.

ellipse

Рис.4.11. Вид A на рис.4.9. При вращении эллипса, проходящего через точку A, его малая полуось изменяется. Радиус-вектор этого эллипса D0 описывает окружность и в некотором положении совпадёт с радиус-вектором C0, поскольку задано D0 = С0.

На этом рисунке мы показываем и главных участников процесс вращения - целевую точку C и "нацеленную" на неё вращаемую точку D эллипсоида. На рисунке без каких-либо особых целей плоскость эллипса AB0 и, соответственно, координатную плоскости x'0y' мы показали под некоторым углом. Ось z' на этом рисунке направлена при этом влево вверх.

Полутоновыми линиями показаны вращаемые эллипсы. Для простоты мы рассматриваем центральное сечение сфероида, поэтому точка A находится непосредственно на линии эллипса-сечения. Также для простоты мы установили, что "совершенно случайно" в этой же плоскости находится и целевая точка C. Следовательно, и точка D также обязана находиться в этой плоскости. Главное обязательное условие совмещения точки D и точки C - это равенство их радиус-векторов R_D0 = R_C0, которое задано условиями задачи. При этом эти векторы R_D0 и R_C0 не обязаны быть равны радиус-вектору R_A0 исходной точки эллипса A. Красной штриховой полутоновой линией показано другое сечение эллипсоида, проходящее через точку B. Показаны несколько положений точки D и несущих её вращаемых эллипсов. Понятно, что в процессе вращения эллипсоида, эллипсов точка D описывает в своей плоскости круг. Поскольку радиус-векторы R_C0 и R_D0 равны, то в некотором положении точки D и C обязательно совместятся. Поскольку нам известны длины и проекции векторов, мы можем определить и угол между этими двумя векторами. Это тот угол, на который нужно повернуть вектор R_D0, чтобы он совместился с вектором R_C0.

В данном случае поворот состоит в геометрическом построении соответствующего эллипса, эллипсоида, что является решением поставленной задачи.

Обратное вращение

Понятно, что полученное решение не является окончательным, поскольку все построения и решения выполнены в повёрнутой, производной системе координат x'y'z'. Для получения окончательного решения необходимо произвести обратное вращение, вернуть точки A, B и C и построенный на них сфероид в исходную систему координат xyz.

Разумеется, можно остановиться и на этом этапе. То есть, мы переходим автоматически в новую систему координат и попросту "забываем" о прежней. В соответствие с обозначениями полюсов на рис.4.4, на наших рисунках ось x' должна иметь обозначения слева: полюс Запад, справа: полюс Восток. Ось y' будет отображать полюса Юг и Север, а ось z', соответственно, полюса Полдень и Полночь.

Для обратного вращения нам необходимо установить связь между системой, полученной при указанном переходе, и исходной системой координат. Очевидно, это обратное вращение, так сказать, глобальный, фундаментальный переход от временных координат x'y'z' к исходным xyz заключается в определении связи между этими двумя координатами, координатными системами. Переход к системе x'y'z' мы произвели в "автоматическом" режиме, до векторных вычислений, до нахождения векторов N₁ и N₂, просто привязав эту систему к эллипсу AB0.

Для определения связи между координатными системами рассмотрим некоторую произвольную точку E и опишем её координаты в исходной системе xyz грани AB0, через её же координаты в повёрнутой системе x'y'z'. Поясним, что эта точка E является обобщённым понятием любой точки, возникающей в наших вычислениях в повёрнутой системе координат x'y'z'. Это, в том числе, и любая точка на создаваемых нами эллипсах и эллипсоидах.

Вектор точки E_r при переходе, как и любой другой вектор, не меняет свою длину. Более того, мы имеем право объявить все длины векторов и геометрические параметры треугольников инвариантами при таких переходах. Это значит, что треугольник, эллипс AB0 выглядит одинаково и в системе xyz, и в системе x'y'z'. Именно это обстоятельство, эта инвариантная связь даёт нам возможность установить взаимную зависимость координат точек в каждой из систем. Можно условно, аллегорически сказать, что треугольник AB0 имеет "двойное гражданство". Координаты его вершин можно представить в виде двух эквивалентных таблиц, схожих по виду с матрицами

ellipse

Напомним, что в процессе первого варианта перехода к повёрнутой системе координат при построении векторов N₁ и N₂ мы использовали их координаты в исходной системе xyz. Иначе говоря, нам известны x-y-z координаты всех этих векторов - N₁, N₂ и А0. Следовательно, через вычисления нам также известны углы между этими векторами, в том числе и угол (ψ+β) между N₂ и A0 на рис.4.6. Далее, используя уравнения для построения эллипса (2.2), (2.3) и (2.7), проходящего через две точки, заданные их радиусами A0 и B0 и углом γ между радиусами, мы вычислили угол α наклона вектора A0 к большой оси эллипса. Этим мы определили направление большой оси эллипса в качестве новой оси x', которая, как выше отмечено, заменила в этой роли направление вектора N₂.

Таким образом, нам известны все величины, необходимые для преобразования координат точки E в новых осях - E_x', E_y' и E_z' в координаты исходной системы - E_x, E_y и E_y. Действительно, по координатам в системе x'y'z' мы находим инвариантные длины отрезков EA и EB, формально используя точки A и B как реперные, координатные. Тем самым мы получаем для этой произвольной точки E пирамиду - ABE0 с известными длинами рёбер в повёрнутой системе координат.

Но эта же самая пирамида находится и в исходной системе координат как инвариант. Следовательно, по длинам её рёбер мы можем найти все её параметры, в том числе, и координаты точки E(x,y,z). Полные, развёрнутые уравнения таких преобразований мы приводить не будем. Уравнения для определения этих величин не являются уникальными, хотя, видимо, и не тривиальны.

В заключение приведём краткое описание рассмотренного алгоритма построения эллипсоида в исходной системе координат. По приведённым в работе базовым уравнениям мы строим "повёрнутый" эллипсоид, сфероид в системе координат x'y'z'. Очевидно, что это построение мы производим по точкам: вычисляем очередную точку эллипсоида, сфероида и наносим её на рисунок. Для построение эллипсоида в исходной системе мы сначала пересчитываем x'y'z' координаты этой точки в исходные xyz-координаты, после его наносим эту точку, теперь уже на рисунок в исходных координатах. Это и есть решение поставленной задачи: построение в исходном шаре Римана эллипсоида, сфероида, проходящего через три произвольно заданные точки.

5. Геометрические тела в сфере Римана

Ранее для построения двухмерных геометрических фигур на диске Римана мы использовали уравнения отрезков геодезических, дуг эллипсов - отрезков наикратчайших линий. Подобные же построения, очевидно, осуществимы и в шаре Римана, для чего теперь следует использовать геодезические поверхности, поверхности наименьшей площади. На плоской поверхности мы можем привести эти объекты только в виде аксонометрий. Приведём примеры объёмных тел внутри сферы Римана, используя те же механизмы, уравнения, что и на диске Римана. Теперь эти фигуры не являются двухмерными: это, повторим, аксонометрии трёхмерных геометрических тел.

Тетраэдр (пирамида)

ellipse

Рис.5.1. Эллиптический тетраэдр

Как и треугольник на плоскости, тетраэдр, пирамиду можно считать наипростейшей фигурой, состоящей из геодезических, условно прямых линий. Тетраэдр на рисунке представлен в трёх видах: состоящим из полноразмерных эллипсов, на которых рёбра просто выделены; скелет - это тот же тетраэдр, рёбра которого приведены в евклидовом трёхмерном пространстве погружения; наконец, на третьем рисунке тетраэдр представлен в виде аксонометрии без всяких вспомогательных линий.

Куб

На следующем рисунке представлена аксонометрия куба в двух вариантах. Сначала для наглядности строим в границах диска Римана аксонометрию в обычном декартовом виде. Затем эти же точки соединяем геодезическими, отрезками эллипсов.

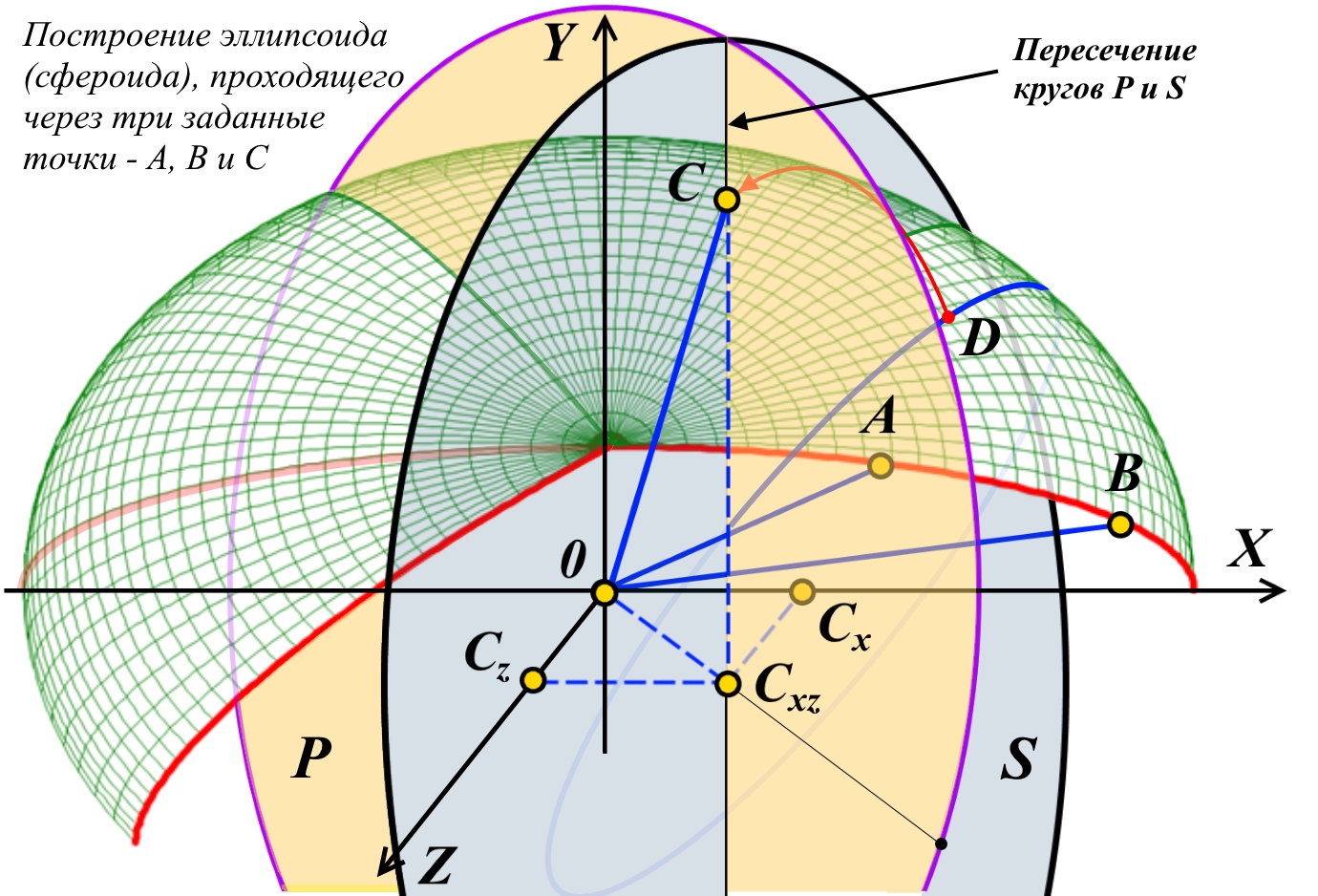
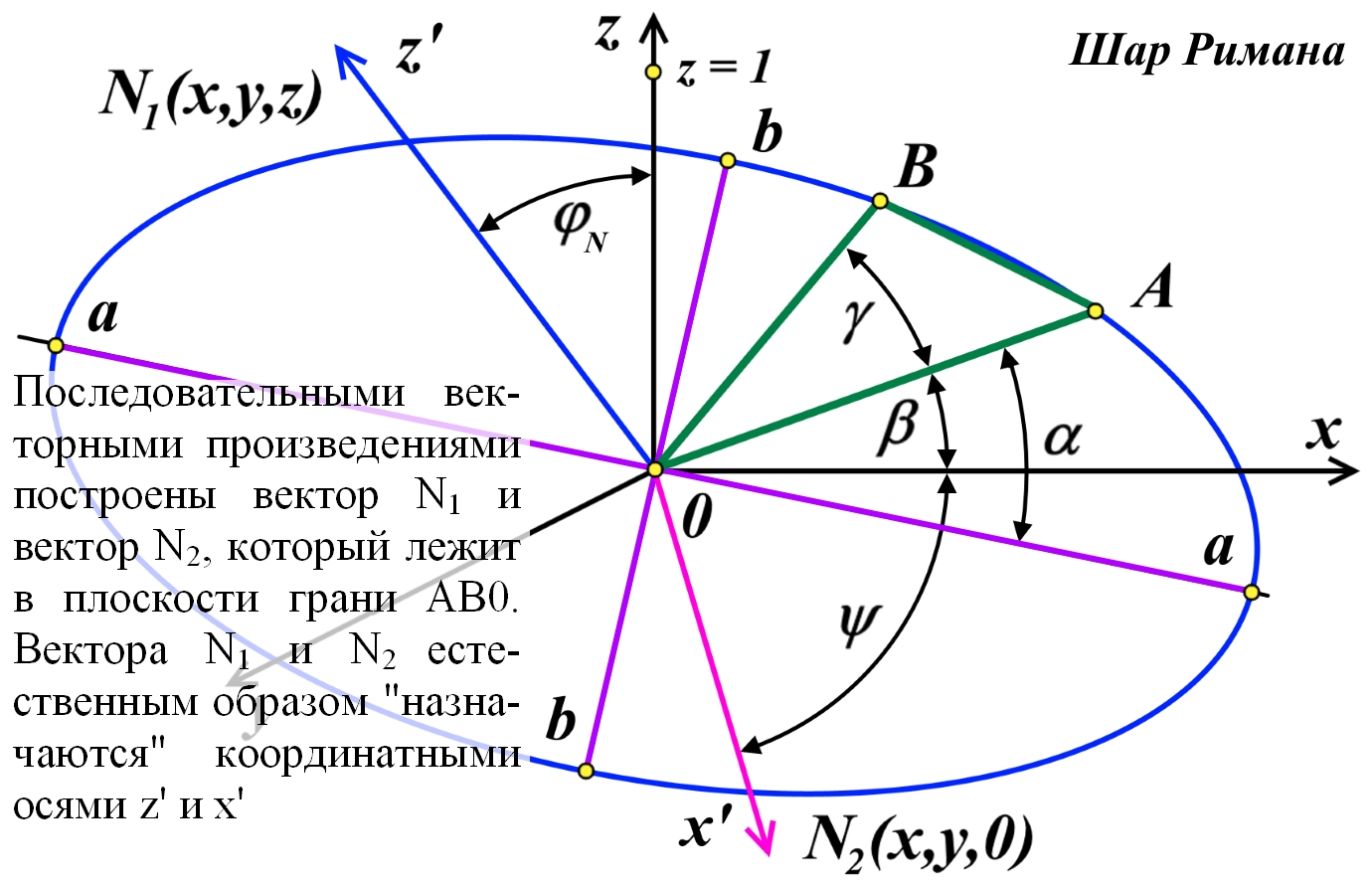
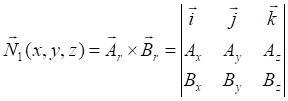
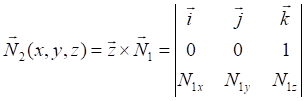
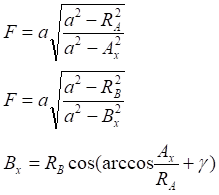
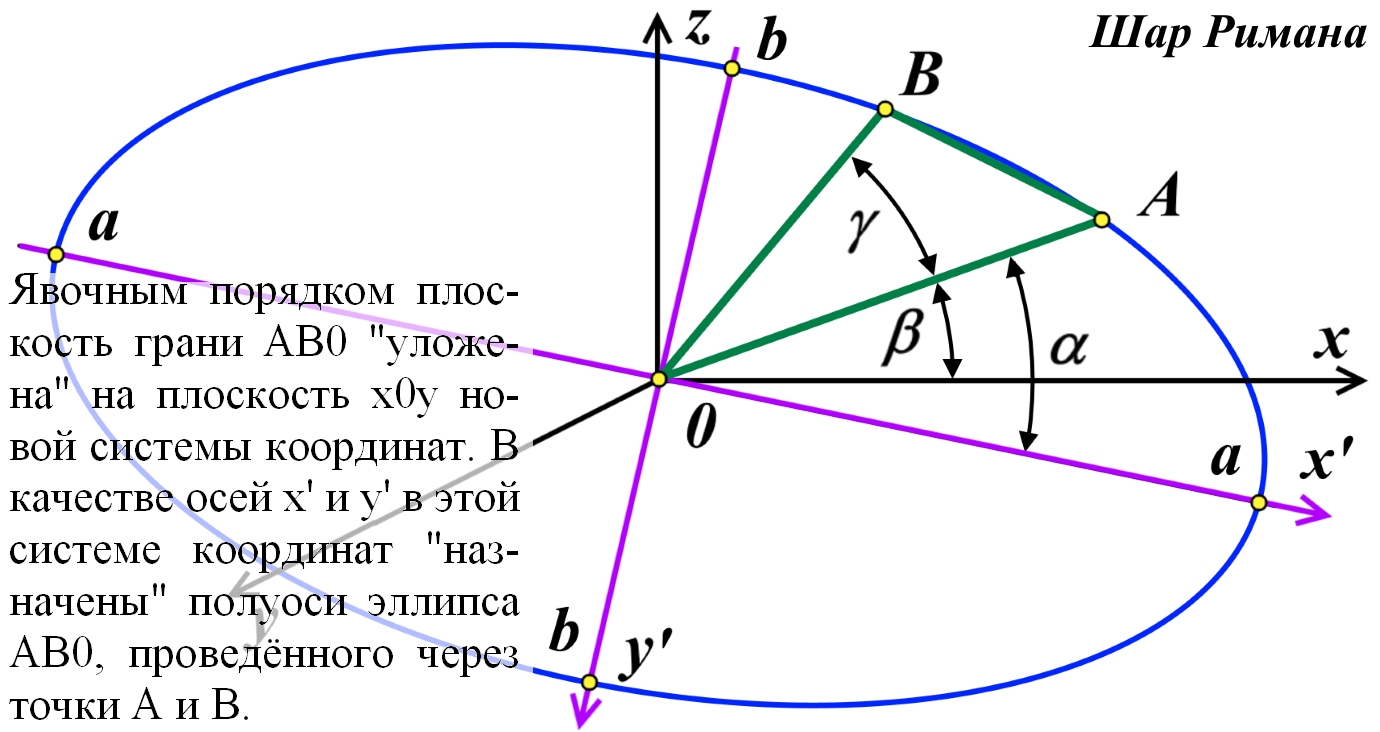
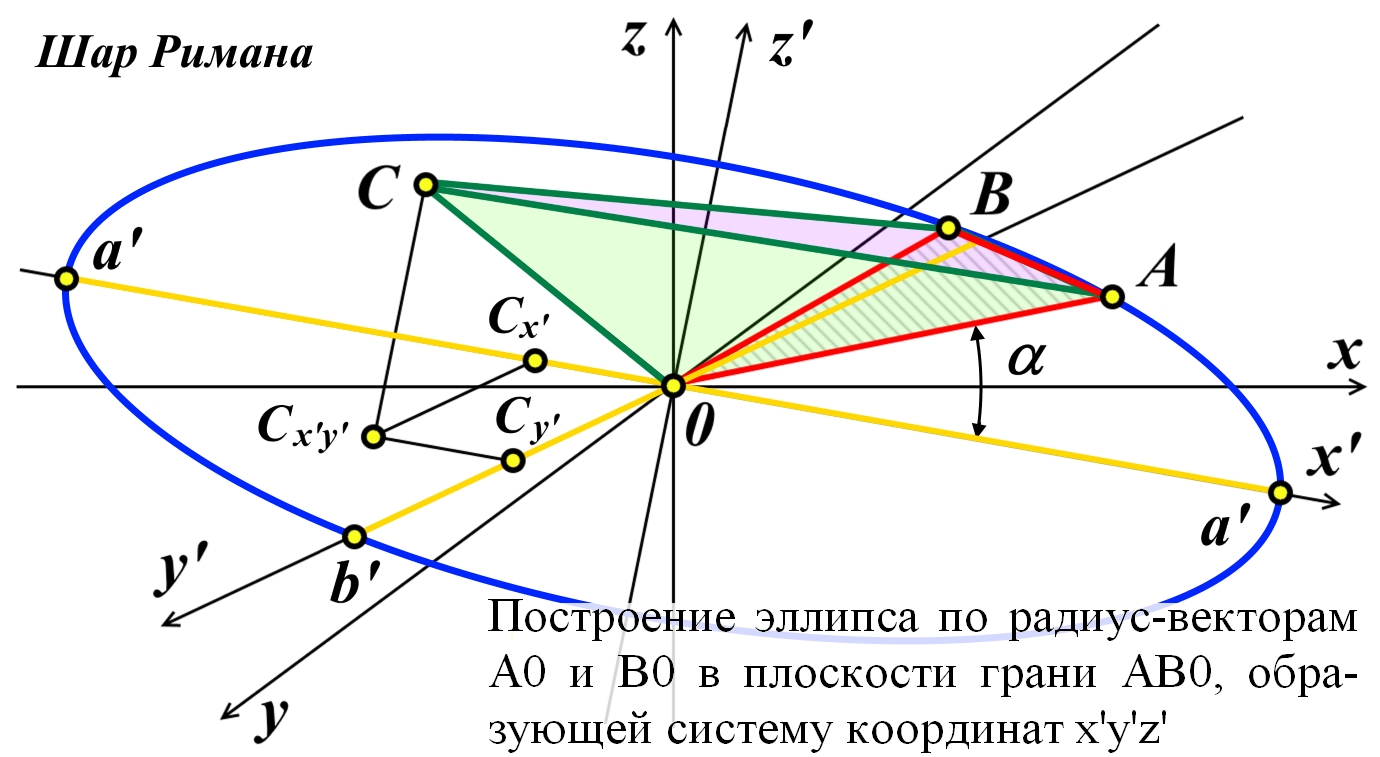
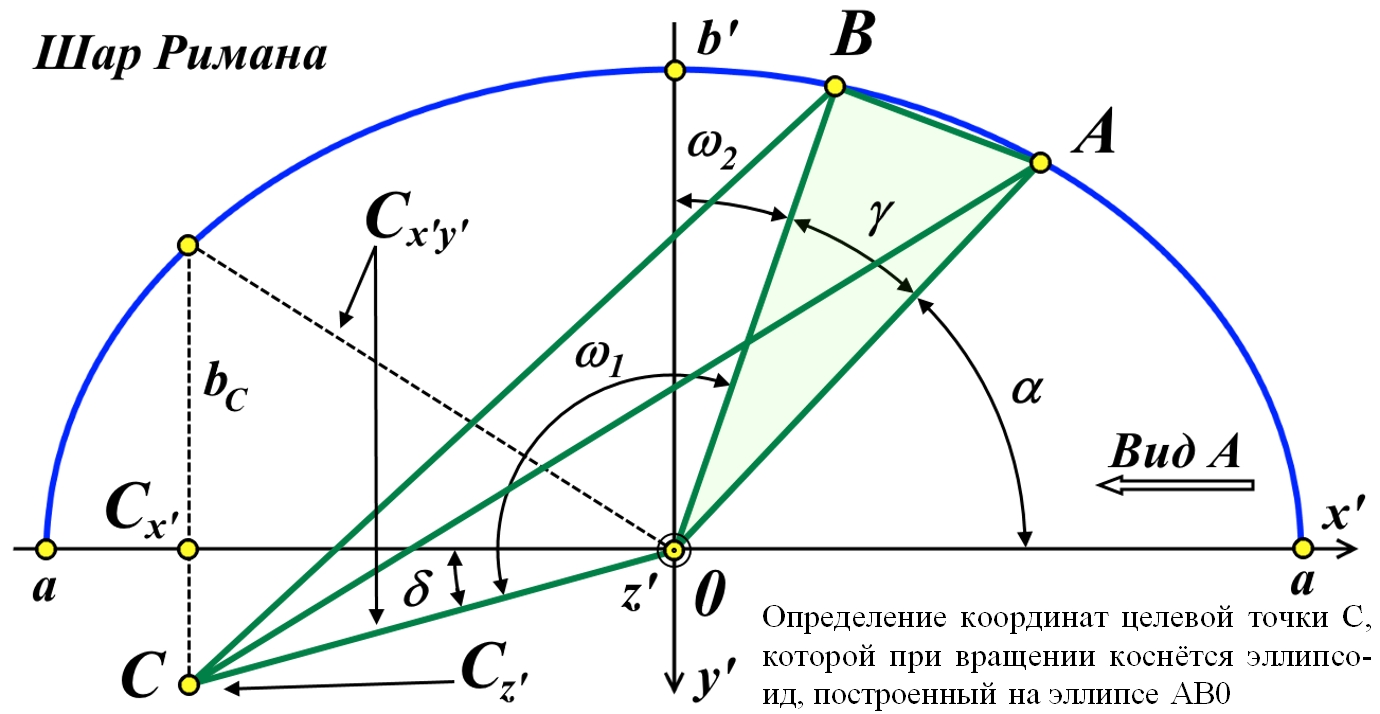
ellipse

Рис.5.2. Эллиптический куб

Гиперкуб

ellipse

Рис.5.3. Эллиптический гиперкуб

Традиционное изображение гиперкуба, тессеракта. Мы привели два варианта: декартову аксонометрию "скелета" и эллиптическую аксонометрию на диске Римана. Точно так же эллиптическая аксонометрия гиперкуба будет выглядеть и в шаре Римана.

Фигуры мы умышленно изобразили с небольшим наклоном, чтобы по возможности избежать радиальных отрезков эллипсов, которые будут представлены не дугами, а строго прямыми линиями.

Заключение

Диск (круг) Римана - это симуляция двухмерного эллиптического пространства положительной кривизны. Обозначение его как симуляции означает, что это двухмерное пространство лишь отчасти отражает все свойства оригинала, поскольку оно не позволяет увидеть, что собой реально представляет этот оригинал. Диск Римана можно назвать проекцией на плоскость эллиптического двухмерного пространства, в рассматриваемом случае - сферической поверхности. Вероятно, возможны ещё две проекции эллиптического пространства -проекция сфероида вращения вдоль оси вращения и проекция произвольного эллипсоида. В последнем случае диск Римана примет форму плоского эллипса. Считать диск Римана конформным отображением соответствующего пространства нельзя, поскольку в проекции последнего углы не сохраняются. Это хорошо видно, например, на рис.3.2.

Сфера (шар) Римана - это симуляция трёхмерного эллиптического пространства положительной кривизны. Такое пространство требует введения особой категории геодезических. Здесь это не геодезическая линия, а геодезическая поверхность. Обозначение сферы как симуляции также означает её неполное соответствие оригиналу, суть которого также неясна. Сфера, шар Римана позволяет наглядно показать некоторые соотношения в реальном эллиптическом трёхмерном пространстве, но и она не является в полной мере конформным отображением.

Эллиптические симуляции позволяют выдвинуть следующие предположения, справедливость которых, строго говоря, нуждается в доказательстве:

Через вершины треугольника можно провести любое число эллипсоидов. Через вершины треугольника можно провести любое число двухосных эллипсоидов - сфероидов, то есть, эллипсоидов две оси которого равны и в данном контексте - предопределены. Если третья ось имеет некоторое заданное значение, то соответствующий полу-сфероид единственный.

Если вершина треугольника совпадает с центром эллипса, то через две его другие вершины можно провести только два эллипса (симметричные эллипсы считаем одним). Если эти вершины лежат по одну сторону от большой оси эллипса, то такой эллипс - единственный.

Разработан алгоритм и уравнения для построения на диске Римана геометрических фигур, состоящих из геодезических. Рассмотрен аналогичный алгоритм, но без законченного набора уравнений, для построения в шаре Римана геометрических тел, ограниченных геодезическими поверхностями.

Литература

1. Вращение эллипса, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/rotatellips.shtml

2. Иллюзия кривизны (проект). Самиздат, URL: http://samlib.ru/p/putenihin_p_w/illusio.shtml

3. Парадоксы параллельности (проект), Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/paraldox.shtml

4. Путенихин П.В. Логические основания многомерных пространств. -- Саратов: "АМИРИТ", 2018. - 396 с., цв. илл.

5. Трёхмерное пространство отрицательной кривизны. Сфера Лобачевского, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/sphelobach.shtml

6. Трёхмерное эллиптическое пространство положительной кривизны. Диск и шар Римана, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/spheriman.shtml

21.11.2021 - 04.01.2022

Оставить комментарий © Copyright Путенихин Петр Васильевич (pe_put@rambler.ru) Размещен: 04/01/2022, изменен: 04/01/2022. 97k. Статистика. Статья: Естествознание Геометрия Иллюстрации/приложения: 125 шт. Скачать FB2		Ваша оценка:
Аннотация: Решена задача построения эллипса, проходящего через две точки. Решена задача вращения эллипса вокруг его центра на любой угол. Введены понятия диска Римана - симуляции эллиптического двухмерного пространства, и шара Римана - симуляции трёхмерного эллиптического пространства. Введено понятие геодезической поверхности. Разработаны алгоритмы и уравнения для построения геометрических фигур на диске Римана, из отрезков геодезических. Этот же алгоритм позволяет строить аксонометрии трёхмерных тел в эллиптическом пространстве шара Римана. Two-dimensional and three-dimensional elliptic spaces of positive curvature are investigated by the example of a disk (circle) and sphere (ball) of Riemann. The Riemann disk can be called a projection onto the plane of an elliptic two-dimensional space, in this case, a spherical surface. In two-dimensional spaces, geodesics are the shortest lines. Three-dimensional elliptic space of positive curvature presupposes the introduction of a special category of geodesics - geodesic surfaces. A solution is given to the problem of drawing an ellipse through two points on the Riemann disk. An algorithm for constructing a spheroid passing through three points in the ball of Riemann is investigated.

Путенихин Петр Васильевич Трёхмерное эллиптическое пространство положительной кривизны. Диск и шар Римана

Путенихин Петр Васильевич
Трёхмерное эллиптическое пространство положительной кривизны. Диск и шар Римана