Путенихин Петр Васильевич. Вращение эллипса

Рассмотрим задачу на построение эллипсов.

Задан круг радиуса R, в котором нарисован эллипс с большой полуосью a = R, расположенной горизонтально, и произвольной малой полуосью b. Требуется повернуть этот эллипс вокруг центра круга на произвольный угол φ.

Каноническое уравнение эллипса имеет вид

Поскольку сумма квадратов равна единице, представим её как сумму квадратов синуса и косинуса некоторого отвлечённого параметра

Разделим попарно переменные по смыслу

Это равенство, видимо, равно также и квадрату некоторой другой, третьей величины

Или в другом, раздельном виде

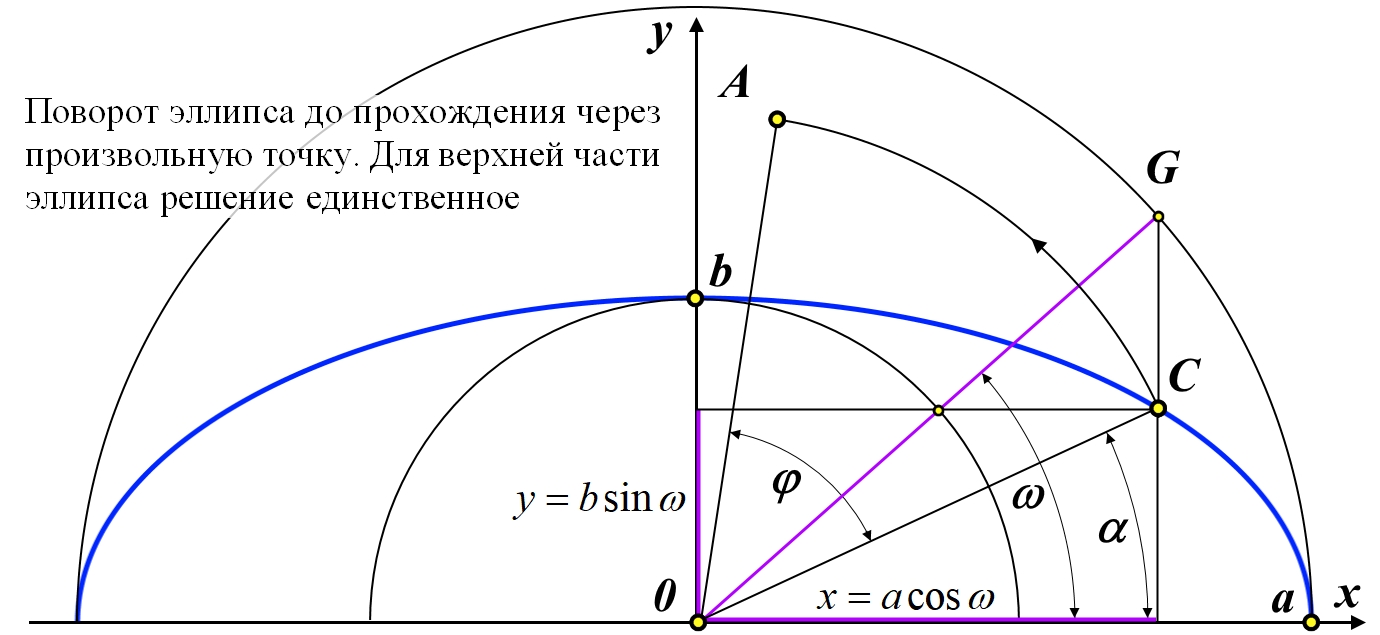
rotate ellipse

Преобразуем

rotate ellipse

Возможны несколько вариантов. Первый: S = 0

Отсюда получаем традиционную систему параметрических уравнений эллипса с центром в начале координат

Второй простейший вариант удобно рассмотреть для единичного значения константы S = 1

Уравнения выглядят достаточно близко к параметрическим

rotate ellipse

Такую систему параметрических уравнений следует, видимо, отнести к некоторому мнимому объекту. Однако в настоящий момент этот вариант интереса для нас не представляет. Третий вариант можно представить в расширенном параметрическом виде

rotate ellipse

Преобразуем

rotate ellipse

К этой системе уравнениям есть смысл добавить и введённое значение переменной S, представив её как третью координату

rotate ellipse

Три уравнения этой системы описывают некое тело в трёхмерном пространстве. Для каждого значения параметра c мы получаем соответствующую систему уравнений. При нулевом значении - это обычное параметрическое уравнение эллипса. При меняющемся значении параметра ω, система выглядит как описание какой-то волнообразной "спирали", спирали с переменной амплитудой вдоль оси z.

Есть ещё один, четвертый вариант. Рассмотрим вновь каноническое уравнение эллипса (1)

rotate ellipse

Выделяем две смысловые группы и преобразуем

rotate ellipse

В результате получаем "каноническое" уравнение

rotate ellipse

Судя по всему, это уравнение описывает своеобразную "эллиптическую" двухстороннюю воронку с главной осью вдоль оси x. Каждое сечение этого объекта ортогонально оси x даёт эллипс, радиусы которого возрастают квадратично по мере удаления от центра системы координат.

rotate ellipse

Для решении поставленной задачи нам понадобятся каноническое (1) и параметрические (2) уравнения. Для удобства будем рассматривать верхнюю половину эллипса. Этот выбор вы обосновываем тем, что в системе координат Земли, на сфере рассматриваются обычно не большие круги, а только их половины - меридианы. Зафиксируем на построенном эллипсе некоторую точку C. Проведём к этой точке линию из центра круга. Для определённости назовем эту линию 0C радиусом C эллипса, подразумевая его полное название - радиус-вектор эллипса в точке C. Согласно параметрическим уравнениям эллипса, координаты его точек определяются системой

При вращении эллипса все его точки, в том числе и C, останутся на неизменном удалении от центра. Как видим на рисунке, линия эллипса образуется движением некоторой точки G по внешнему радиусу круга. При этом координаты точек эллипса образуются как проекции двух разных окружностей. Можно заметить, что при другой комбинации проекций будет построен ортогональный эллипс.

Квадрат длины введённого радиус-вектора C равен

Угол α назовём углом радиуса C. Величину угла определим из соотношения

rotate ellipse
Рис.1. Поворот эллипса до прохождения через произвольную точку. Для верхней части эллипса решение единственное

Для поворота эллипса вокруг центральной точки на некоторый произвольный угол φ, вычислим координаты всех его точек как проекции всех повернутых радиусов эллипса. В результате такого поворота на угол φ, координаты точки C изменятся, то есть перейдут в некоторую пока неизвестную нам точку A:

Решим эту систему совместно с уравнением (3)

Подставим в эту систему уравнений значение найденного угла α из (4), в результате чего получим систему, содержащую только переменный параметр ω и известные величины

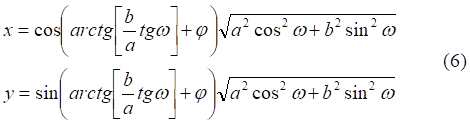
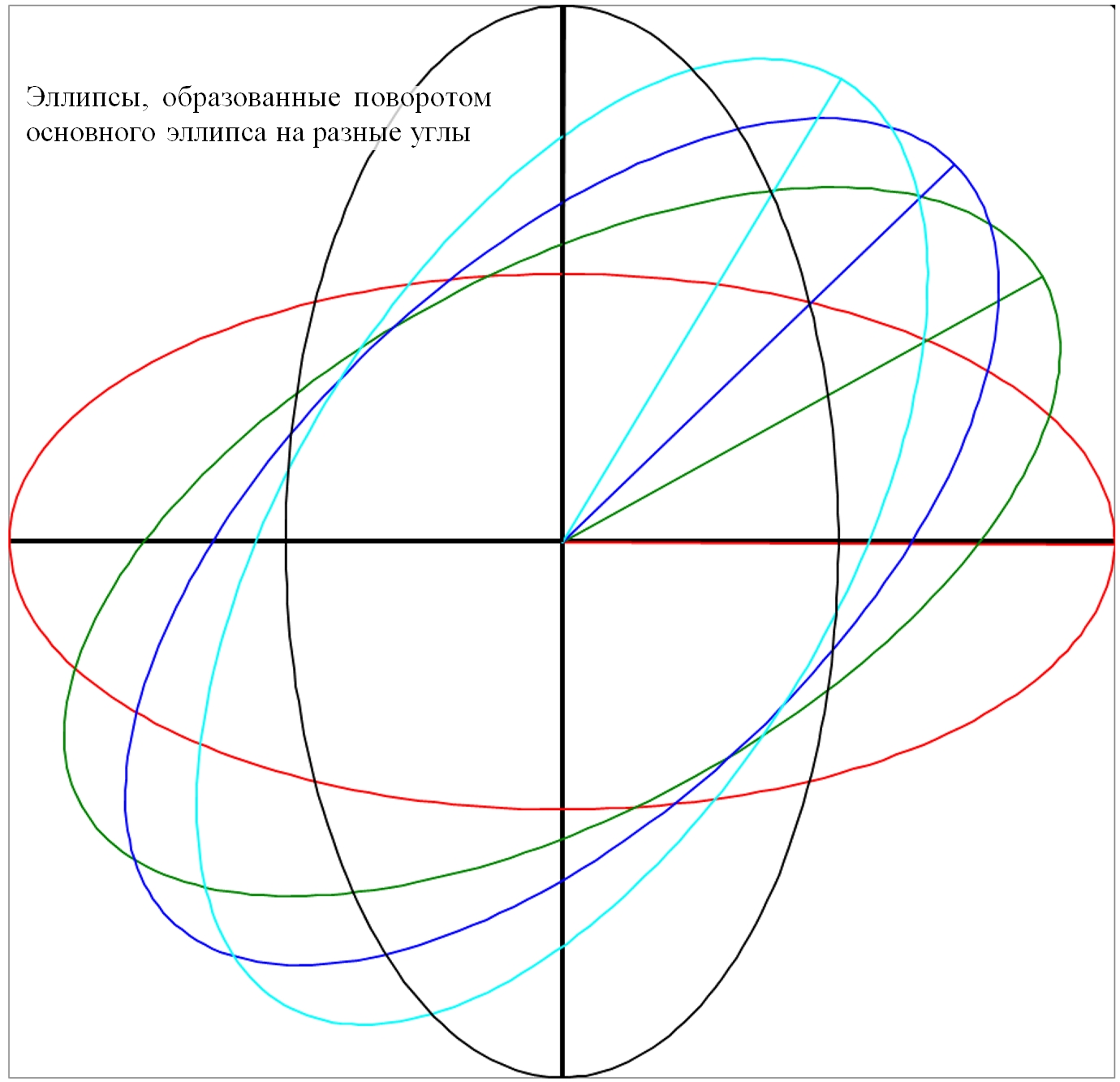
rotate ellipse

Полученная система позволяет повернуть эллипс с полуосями (a = R, b) на произвольный угол φ. На следующе рисунке представлены эллипсы, повёрнутые на разные углы с помощью полученной системы уравнений

rotate ellipse
Рис.2. Эллипсы, образованные поворотом основного эллипса на разные углы

Сформированная система уравнений позволяет повернуть эллипс на любой угол. Но она также позволяет решить и обратную задачу: определить угол поворота, при котором эллипс пройдёт через заранее заданную произвольную точку.

Очевидно, что через любую точку можно провести неограниченное число эллипсов. Поэтому мы рассмотрим более жёсткие условия, частный вариант эллипса, заданного обеими своими осями. Можно заметить, что таких эллипсов существует только два, поскольку кривая замкнута. Поэтому для однозначности вновь будем рассматривать только половину эллипса, его верхнюю дугу.

Легко заметить, что эллипс с указанными характеристиками может пройти только через точки, находящиеся в области кольца, образованного его радиусами.

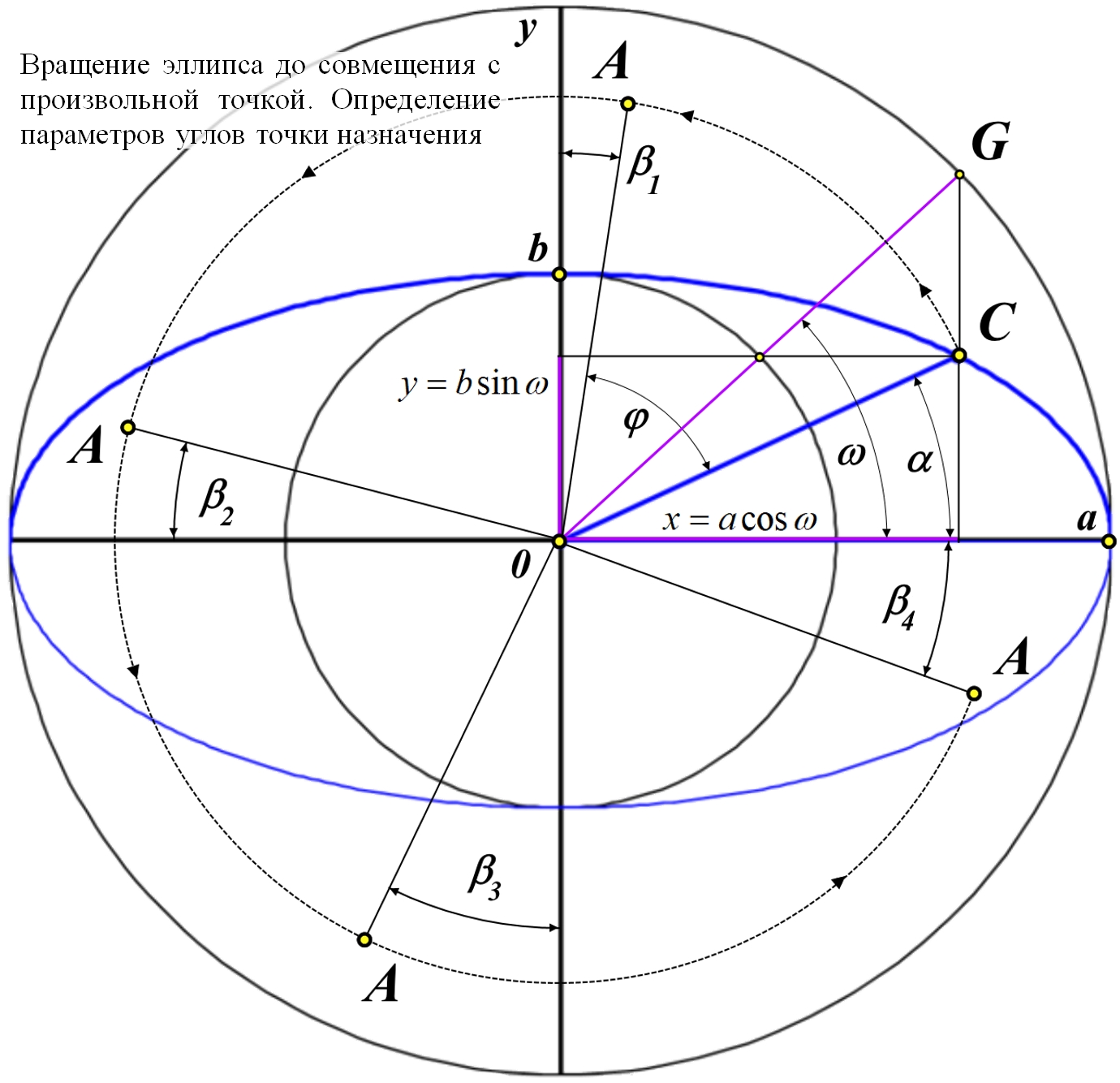
rotate ellipse
Рис.3. Вращение эллипса до совмещения с произвольной точкой. Определение параметров углов точки назначения

Процесс вращения означает движение точки C эллипса в точку A. Длина радиуса C0 при этом равна длине радиуса A0

Угол φ между векторами - это искомый угол, на который нужно повернуть эллипс для его прохождения через точку A. Очевидно, этот угол зависит от того, в каком квадранте находится точка A. Действительно, для каждого из квадратнов запишем

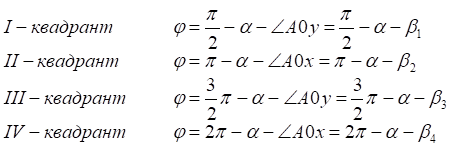
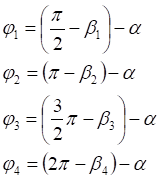
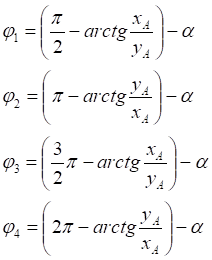
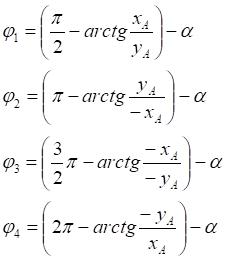
rotate ellipse

Эти разнообразные определения угла φ желательно свести к некоторой единой системе. Для создания такой системы изменим запись уравнений. Для всех четырёх квадрантов получаем

rotate ellipse

Для определения характеристик углов β, расшифруем их, представим в координатах соответствующих точек A

rotate ellipse

Далее для наглядности пометим значками минуса отрицательные координаты. Подчеркнём, в данном случае эти значки просто обозначают, что соответствующая координата имеет отрицательное значение

rotate ellipse

Из этих расшифровок выводим условия использования той или иной строки определения угла в скобках:

1. x > 0, y > 0

2. x < 0, y > 0

3. x < 0, y < 0

4. x > 0, y < 0

Теперь мы должны взять положительные значения, модули дробей под функциями арктангенса

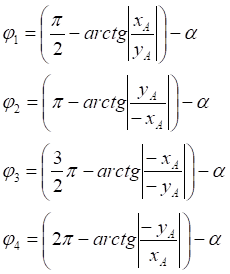
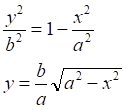
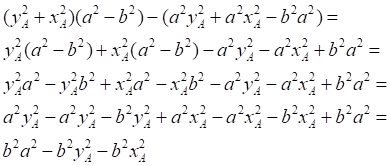
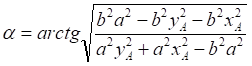
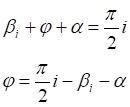
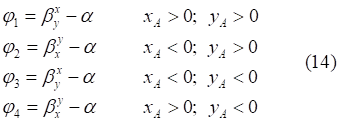
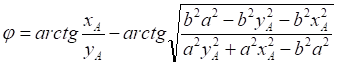
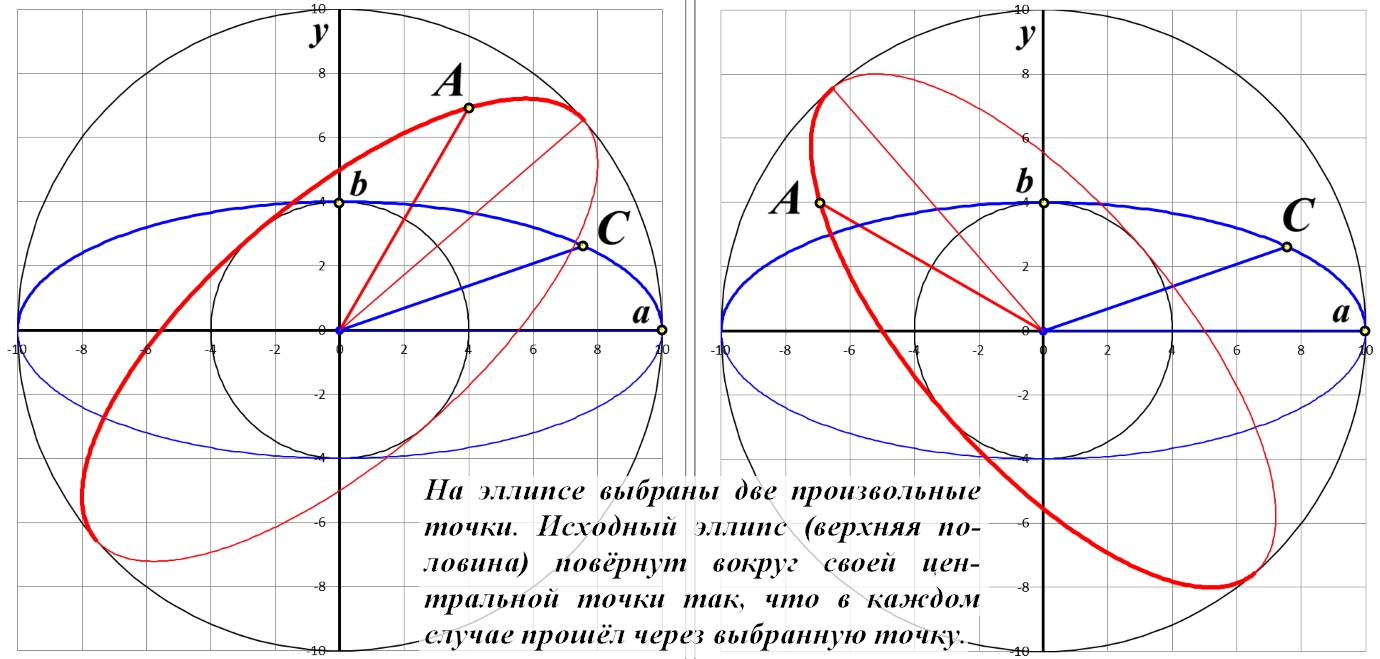
rotate ellipse

С учётом модулей под знаками арктангенсов введём новые обозначения Дополним запись условиям знаков координат x_A и y_A. Углы β, представленные арктангенсами, в уравнении разные, поэтому обозначим их индексами, означающими, какая координата в дроби под арктангенсом находится сверху, а какая - снизу.

rotate ellipse

Уточним: верхний и нижний индексы не имеют обычного математического смысла, это просто метки, что в соответствующей функции арктангенса числителем и знаменателем являются координаты, занимающие соответствующее индексу место.

Поскольку координаты точки A заданы по условиям задачи, этот угол β также однозначно определён. Второй угол - α позволяет определить значение параметрического угла ω, который и образует вращаемый вектор C0. Рассмотрим каноническое уравнение эллипса

После преобразований получаем

rotate ellipse

Используем это уравнение в условии равенства исходного радиуса C0 и радиуса A0, в который он должен переместиться

Преобразуем

rotate ellipse

Из уравнений (10) и (9) находим вторую координату

rotate ellipse

Уравнения (11) и (12) содержат только известные величины, поэтому из них мы можем найти угол α

rotate ellipse

Преобразуем

Упростим выражение в числителе под корнем

rotate ellipse

Подставляем предыдущее, исходное уравнение

rotate ellipse

На рисунке можно увидеть, что в общем случае, для всех вариантов расположения точки A для i = 1...4 справедливо равенство, из которого находим угол φ

rotate ellipse

Сравниваем это выражение с (8) и исправляем последнее

rotate ellipse

Подставляем вычисленные параметры и определяем искомый угол поворота φ

rotate ellipse

Используя это уравнение угла, мы можем повернуть эллипс, заданный полуосями (a = R, b) до прохождения его через точку A. На следующем рисунке представлены два таких вращения

rotate ellipse
Рис.4. На эллипсе выбраны две произвольные точки. Исходный эллипс (верхняя половина) повёрнут вокруг своей центральной точки так, что в каждом случае прошёл через выбранную точку.

Литература

1. Путенихин П.В. Вращение эллипса, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/rotatellips.shtml

17.11 - 21.11.2021

Оставить комментарий © Copyright Путенихин Петр Васильевич (pe_put@rambler.ru) Размещен: 20/11/2021, изменен: 20/11/2021. 15k. Статистика. Статья: Естествознание Геометрия Иллюстрации/приложения: 47 шт. Скачать FB2		Ваша оценка:
Аннотация: Рассмотрена задача построения эллипса по параметриче-ским уравнениям. Решена задача вращения эллипса вокруг его центра на любой угол. Решена задача проведения заданного эллипса через произвольную точку в области кольца с радиусами его полуосей. Существует единственный меридианальный эллипс (верхняя половина), проходящий через такую точку. The problem of constructing an ellipse from parametric equa-tions is considered. Solved the problem of rotating an ellipse around its center at any angle. The problem of drawing a given ellipse through an arbitrary point in the region of the ring with the radii of its semiaxes is solved. There is a single meridian ellipse (upper half) passing through such a point.

Путенихин Петр Васильевич Вращение эллипса

Путенихин Петр Васильевич
Вращение эллипса