Мак Петр Анатольевич. Вг2

ПЕРЕНОС ТРИАНГУЛЯЦИОННОЙ СЕТИ С ПОВЕРХНОСТИ ЭЛЛИПСОИДА НА ПЛОСКОСТЬ В ПРОЕКЦИИ ГАУССА -- КРЮГЕРА

Перенос триангуляционной сети с поверхности эллипсоида на плоскость заключается, в конечном счете, в переходе от эллипсоидальных треугольников к плоским с прямолинейными сторонами и в получении координат Гаусса -- Крюгера для всех пунктов сети.

Первоначальными исходными данными для построения триангуляционной сети являются широты и долготы одного или нескольких пунктов, длины базисных сторон и их азимуты и измеренные на местности углы (направления). Перенеся эти элементы триангуляции по правилам проекции на плоскость, координаты всех остальных пунктов триангуляционной сети получают вычислениями на плоскости.

Таким образом, переносят триангуляционную сеть с поверхности эллипсоида на плоскость в такой последовательности:

1) по известным широтам и долготам исходных пунктов вычисляют их прямоугольные координаты;

2) на концах базисных сторон вычисляют Гауссово сближение меридианов и дирекционные углы базисных сторон;

3) редуцируют на плоскость длины базисных сторон;

Редуцирование: стороны треугольников триангуляции при переносе с земной поверхности (с поверхности эллипсоида) на плоскость изображаются кривыми, вогнутостью направленными в сторону оси абсцисс. Углы между этими кривыми, считаемые как углы между касательными к кривым в вершине угла, по условию конформности проекции равны измеренным на местности. Чтобы иметь возможность решать треугольники, от криволинейных сторон переходят к прямолинейным, заменяя кривые хордами. Длины прямолинейных сторон практически равны длинам их действительных изображений. Углы в новых треугольниках с прямолинейными сторонами отличаются от углов с криволинейными сторонами, (а, следовательно, и от измеренных на местности), на величины, зависящие от углов между кривыми и хордами. Заменяя кривые (действительные) изображения сторон угла хордами, мы изменяем направления сторон угла на величину поправки к измеренным направлениям при переходе от криволинейного изображения линий, соответствующих этим направлениям, к прямолинейным изображениям.. Поэтому эти углы называются поправками за кривизну изображения геодезических линий на плоскости в проекции Гаусса -- Крюгера или, редукциями направлений. Направления же, в которые введены эти поправки, называются редуцированными на плоскость направлениями.

4) для измеренных направлений вычисляют поправки за кривизну изображения геодезических линий на плоскости и получают редуцированные на плоскость направления и углы.

В заполняющих сетях 3 класса исходными данными являются пункты, для которых известны координаты Гаусса -- Крюгера, поэтому перенос такой сети с поверхности эллипсоида на плоскость сводится только к вычислению поправок за редукцию направлений и в получении редуцированных направлений.

Суммарная поправка в направление вычисляется по формуле:

Значения ?₁ ?₂ ?₃вычисляются до 0?,01 и вводятся в направления, исправленные за центрорвку и редукцию.

1). Поправка за переход от прямого нормального сечения к геодезической линии ?₁

0x01 graphic

2) Поправка за высоту наблюдаемой точки ?₂

где H₂= H⁰₂ + h - высота точки визирования над поверхностью референц-эллипсоида.

3) Поправка за уклонение отвесной линии от нормали к поверхности эллипсоида ?₃

где ?₁и ?₁ - составляющие (проекции) полного уклонения отвесной линии на плоскости меридиана и первого вертикала4

z_1.2 - зенитное расстояние с точки 1 на точку 2

Редуцированная длина базиса триангуляции вычисляется по формуле:

0x01 graphic
,

где s₀ - редуцированная поправка базиса на поверхность референц-эллипсоида;

H⁰_m -средняя высота измеренного базиса над уровнем океана (геоидом), определяется при нивелировании

h - средняя высота геоида над референц-эллипсоидом в месте расположения базиса;

R_?- радиус нормального сечения, в котором расположена линия базиса;

H_m= H⁰_m + h

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ГАУССА -- КРЮГЕРА ИЗ ОДНОЙ ЗОНЫ В ДРУГУЮ

Ходы полигонометрии, проложенные между триангуляционными пунктами, нередко имеют начальный пункт, расположенный в одной зоне, а конечный в другой -- смежной. В триангуляционной сети, подлежащей уравниванию, одна часть пунктов может находиться в одной зоне, а другая в смежной. И в том, и в другом случае часть пунктов будет иметь координаты Гаусса -- Крюгера в одной системе (1-й зоны), а часть пунктов в другой системе (2-й зоны).

Уравнительные вычисления делают в одной системе координат, поэтому часто возникает необходимость еще до уравнивания иметь координаты всех твердых пунктов в системе одной (первой или второй) зоны.

Приходится решать следующую задачу: для пункта известны координаты Гаусса -- Крюгера ху, в зоне с осевым меридианом, имеющим долготу L₁ (1-я зона); требуется вычислить коор- динаты Гаусса -- Крюгера х₁ и у₁ этого пункта в смежной зоне с осевым меридианом, имеющим долготу L₂ = L₁ + l (2-я зона).

Эта задача носит название "преобразование координат Гаусса-- Крюгера из одной зоны в другую" и может решаться различными способами. Рассмотрим некоторые из них.

Первый способ заключается в том, что по известным для пункта координатам х₁ и у₁ пункта Р вычисляют широту В и долготу L, затем по широте и долготе, принимая осевой меридиан 2-й зоны вычисляют искомые прямоугольные координаты вычисляют координаты х₂ и у₂. Способ достаточно прост, но достаточно большой объем вычислений, которые требуют значительного времени, поэтому указанный способ применяют редко, когда нужно преобразовать координаты небольшого числа пунктов с большой точностью.

Второй способ преобразования координат, который целесообразно применять для значительного числа пунктов, основан на переходе от редуцированных направлений и сторон в системе зоны I к направлениям и сторонам на сфероиде, а от них -- к редуцированным направлениям и сторонам в системе зоны II и вычислению искомых координат пунктов в этой зоне по обычным формулам. Могут иметь место некоторые вариации в применении этого способа в зависимости от конкретных условий задачи. Рассмотрим более детально один из типовых случаев.

На рис. 1 изображена триангуляция в виде ряда между твердыми сторонами АВ и CD. Координаты исходных пунктов А и В даны в системе зоны I, а пунктов С и D -- в системе зоны II. Уравнивание ряда должно быть выполнено в одной зоне. После уравнивания координаты пунктов 1--7 должны быть окончательно даны в системе зоны I, а координаты пунктов 4--9 -- в системе зоны II, что обеспечит взаимное перекрытие смежных зон. Так как большая часть ряда расположена в зоне I, то уравнивание следует вести в системе этой зоны.

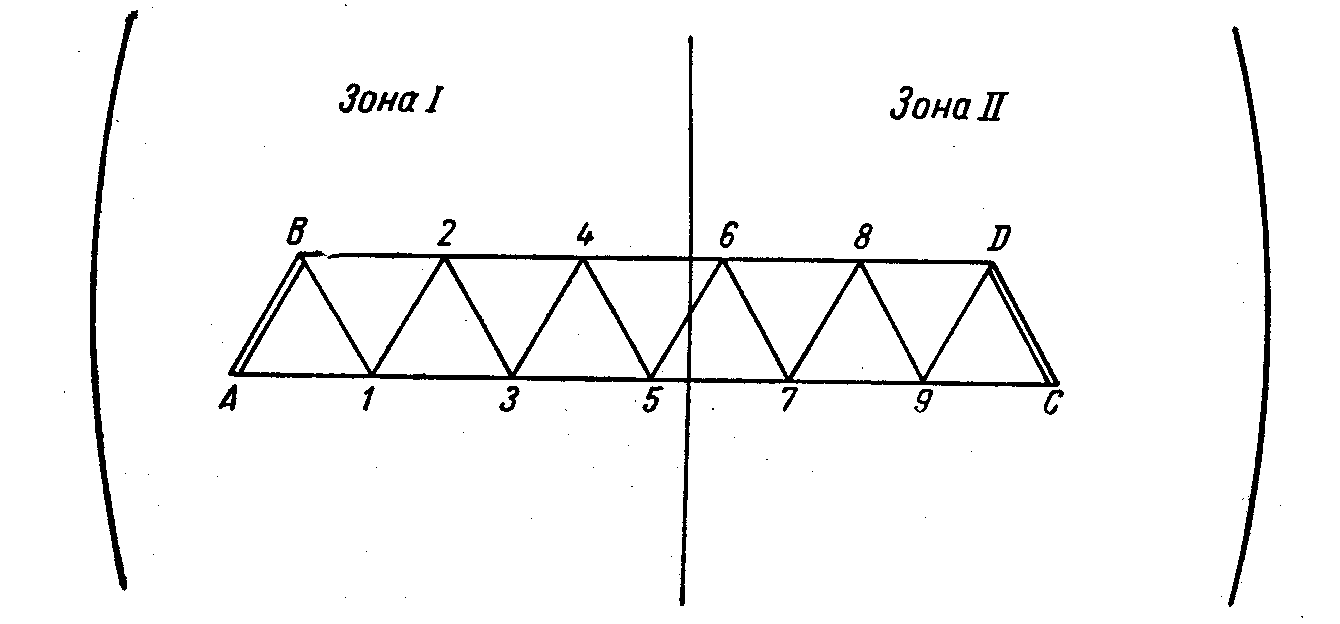
0x01 graphic

Рис. 1

Задача решается в следующем порядке:

а) от координат пунктов С и D, данных в системе зоны II, переходят к координатам в системе зоны I описанным выше способом;

б) вычисляют приближенные координаты всех пунктов ряда, начиная от пунктов А и В в системе зоны I; при помощи этих координат определяют редукции направлений и вводят их в измеренные направления. В результате этих вычислений все элементы ряда получаются отнесенными к системе зоны I;

в) производят уравнивание ряда;

г) из уравненных направлений с пунктов 4 -- 9 вычитают вычисленные редукции направлений и получают, таким образом, уравненные направления на эллипсоиде;

д) по координатам пунктов С и D, отнесенным к зоне II, определяют приближенные координаты пунктов 4 -- 9 и вычисляют редукции направлений с этих пунктов; после введения этих редукций в уравненные сферические направления получают уравненные направления на плоскости с указанных пунктов в системе зоны II;

е) вычисляют окончательно координаты пунктов 1 -- 7 при помощи исходных координат пунктов А и В и уравненных направлений на плоскости, полученных после выполнения (в), и координаты пунктов 4 -- 9 при помощи координат пунктов С и D, отнесенных к системе зоны II, и уравненных направлений на плоскости, полученных в результате выполнения пункта (д).

Таким образом поставленная задача решена. При этом в связи с расположением ряда в двух зонах дополнительной работой явилось приближенное вычисление координат пунктов и редукций направлений для меньшей половины ряда (не считая преобразования координат пунктов В и С по первому способу).

Применение данного способа обеспечивает получение преобразованных координат с полной точностью, соответствующей данному классу триангуляции.

Третий способ (табличный). Большинство других способов основано на применении различного рода таблиц. Из них отметим таблицы, составленные А. М. Вировцем и Б. Н. Рабиновичем. При применении этих таблиц на вычисление отдельного пункта требуется 10 -- 15 минут. Преобразованные координаты получаются с ошибкой до 2 см. Есть таблицы составленные В. Л. Каганом, Е. Е. Бирюковым. Рассматриваемая задача может быть решена при помощи раннее упоминавшихся таблиц А. М. Вировца ("Таблицы координат Гаусса--Крюгера и таблицы размеров рамок и площадей трапеций топографических съемок"). Как указывалось, основное их назначение -- построение в проекции Гаусса рамок трапеций топографических съемок. Эти таблицы содержат также и некоторые вспомогательные данные, позволяющие преобразовывать координаты из зоны в зону с ошибкой порядка 0,2 м.

Формулы, служащие для преобразования координат при помощи указанных таблиц, получаются следующим образом.

Пусть требуется перевычислить координаты пункта А из зоны I в зону II. Обозначим через x₁ , y₁ данные координаты пункта А в зоне I, а через x₂ , y₂ -- искомые координаты в зоне II. Находим трапецию масштаба 1: 25 000, в пределах которой расположен пункт А. На рис. 2 и 3 показано изображение рамок этой трапеции в I и II зонах и изображение пункта А.

Пусть о₁х и о₂х -- изображения прямых, проходящих через юго-западную вершину трапеции и соответственно параллельных осям абсцисс в I и II зонах. От этих прямых отсчитываются дирекционные углы линий. Обозначим координаты вершины трапеции о₂ в зоне II, известные из таблиц, через (x_o)₂ и (у_о)₂. Однако разности координат точек о и А известны только в системе зоны I; обозначим их ?х₁ и ?у₁. Очевидно, несовпадение разностей координат точек о₂ и А₂ с разностями координат точек о₁ и А₁ вызывается различием дирекционных углов и разными значениями масштабов линий о₁А₁ и о₂А₂. Отсюда следует, что разности координат ?х₁ и ?у₁в зоне I могут быть преобразованы в зону II путем учета изменения дирекционного угла линии о₁А₁, которое можно считать вызванным поворотом координатных осей на угол ??.

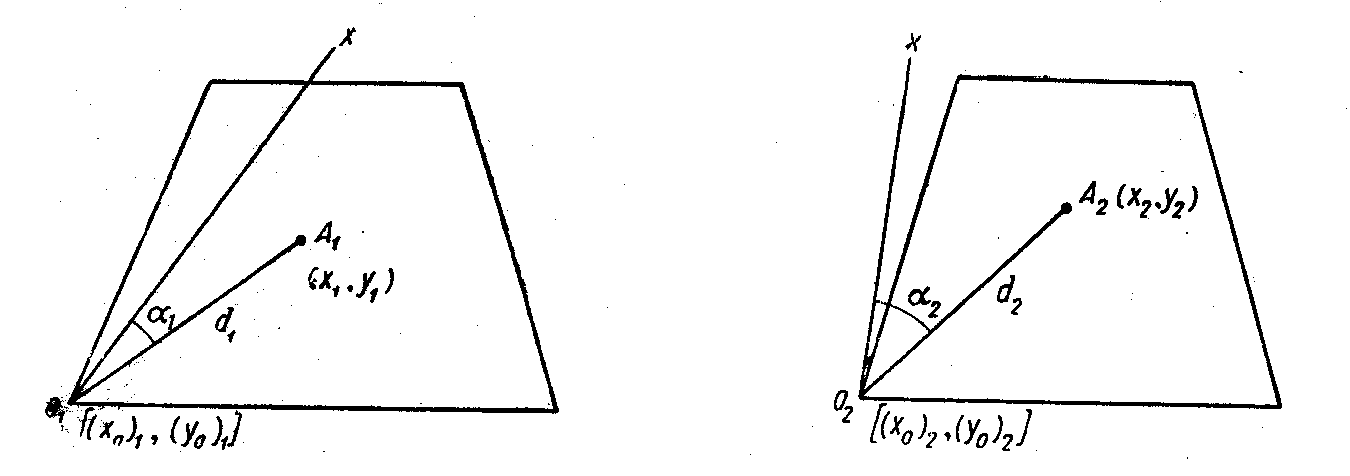
0x01 graphic

Рис. 2 Рис. 3

Затем полученные выражения должны быть исправлены за изменение масштаба ?m при переходе из зоны I в зону II. Следовательно, можно написать:

(1)

0x01 graphic
(2)

Рассмотрим вывод формул, служащих для вычисления ?? и ?m. Введем обозначения:

?₁ -- дирекционный угол линии о₁А в зоне I;

(?_o)₁ --Гауссово сближение меридианов на плоскости в точке о₁ в зоне I;

?₁ -- поправка за кривизну изображения линии о₁А₁на плоскости в зоне I;

d₁ -- расстояние между точками о₁ и А₁ на плоскости зоны I.

Для аналогичных элементов в зоне II имеем обозначения: ?₂, (?_o)₂, ?₂, d₂

Обозначив через А геодезический азимут линии на эллипсоиде, соответствующей прямой о₁А₁ (или о₂А₂) на плоскости, напишем:

для зоны I ?₁= А -- (?_o)₁ -- ?₁,

для зоны II ?₂= А -- (?_o)₂ -- ?₂

откуда

0x01 graphic
. (3)

Далее, имеем:

0x01 graphic

Отсюда, пренебрегая различием между ?х₁ и ?х₂ напишем:

0x01 graphic

Полагая

0x01 graphic

получаем

0x01 graphic
(4)

Построение формулы (4) позволяет для ?? составить таблицу, которая и используется в таблицах Гаусса-Крюгера. Величину ?? выбирают по аргументам ?х и ?у_m_. Значения ? тоже выбирают из таблиц. Следовательно окончательно

?? = (?_o)₁ - (?_o)₁+ ?? (5)

Далее находим изменение масштаба ?m, имеем:

d₁ =sm₁ и d₂ =sm₂ (6)

где m₁ и m₂ -- масштабы изображения для точек о₁ и о₂ в зонах I и II,

s -- расстояние на эллипсоиде, соответствующее расстоянию на плоскости о₁А₁ (или о₂А₂). Из формулы (6) получим:

0x01 graphic

Составляем производную пропорцию:

0x01 graphic

Пренебрегая малым членом 0x01 graphic

получим:

0x01 graphic
(7)

Отношение

и характеризует изменение масштаба при переходе из одной зоны в другую для линии оА, поэтому

0x01 graphic

Чтобы при вычислении иметь дело с меньшим количеством знаков, формулу (7) окончательно переписывается так:

?m = 1 + (m -1)₂ - (m - 1)₁(8)

Величины (m -1)₂ и (m - 1)₁выбирают из вспомогательной таблицы.

Формулы (1), (2), (5) и (8) решают задачу.

В табл. 1 приведен пример на перевод координат из зоны в зону при помощи указанных таблиц.

Пример перевычисления координат из зоны в зону с применением таблиц

Пункт Р задан в зоне N8 координатами x₁ = 5 241 750,0

y₁ = 8 752 000,0

или y₁ =+ 252 000,0

Требуется перевычислить эти координаты в систему зоны N9

Элементы формул	Пункт Р
Элементы формул		От юго-западной вершины трапеции	От юго-восточной вершины трапеции
B l₁^* l₁^** x₁ (x₀)₁ ?x₁ y₁ (y₀)₁ ?y₁ (?₀)₁ (?₀)₂ (?₀)₁- (?₀)₂ ?? ?? sin ?? cos ?? (m - 1)₂ (m - 1)₁ ?m = (m - 1)₂- (m - 1)₁ (x₀)₂ ?x₂ x₂ (y₀)₂ ?y₂ y₂	47?15 ? 3 15 -2 45 5 241 750,0 5 240 259,9 + 1491,1 + 252 000,0 246 020,5 + 5 979,5 2?23 ?16? - 2 01 12 4 24 28 -1 +4 24 27 0,07685 0,99704 517 762 0,999755 +1027,2 +6076,4 5 238 802,4 +1026,9 5 239 829,3 - 208 173,7 +6 074,9 202 098,8	3?22 ?30? -2 37 30 5 241 750,0 5 240 661,1 +1089,9 +252 000,0 255 482,0 -3 482,0 2?28 ?47? - 1 55 42 4 24 29 -1 +4?24 ?28? 0,07685 0,99704 495 791 0,999704 +1353,3 -3388,0 5 238 476,3 +1352,9 5 239 829,2 -198 711,8 -3 387,0 -202098,8

l₁^*- для зоны N8, l₁^**- для зоны N9

Оставить комментарий © Copyright Мак Петр Анатольевич Размещен: 26/05/2016, изменен: 26/05/2016. 30k. Статистика. Глава: Проза Иллюстрации/приложения: 2 шт.		Ваша оценка:

Мак Петр Анатольевич : другие произведения.

Вг2