Аксиома 1. Закон наименования
^ Значение именования произведенного повторно остается -(тем же) значением именования.




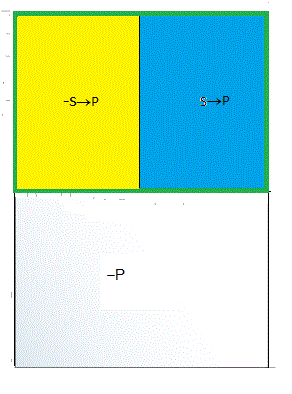

- --
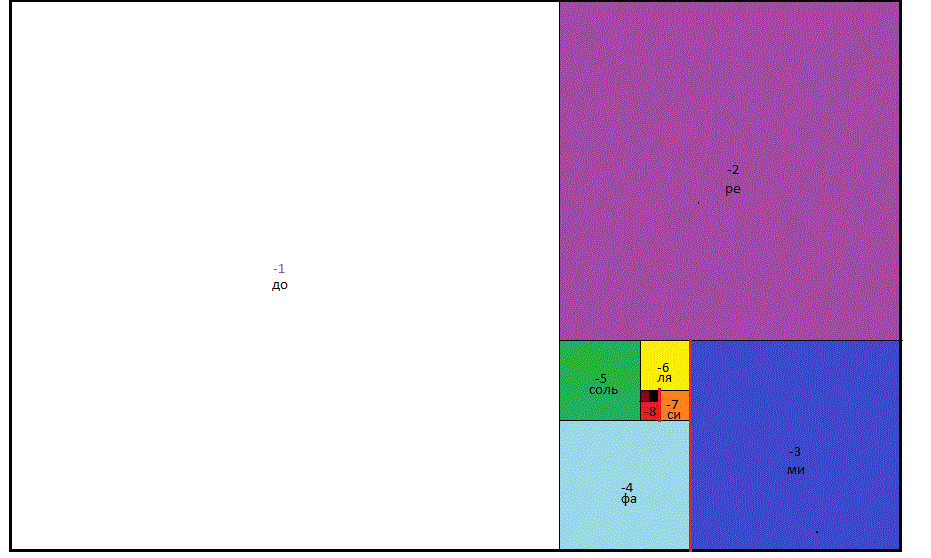
Мы насчитали 9 полей. (по количеству известных однозначных цифр).
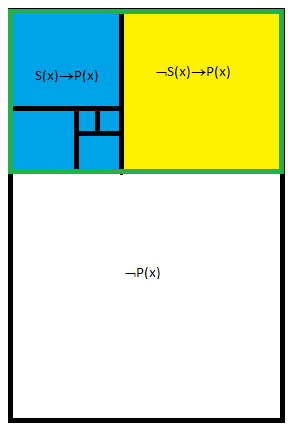
- -- Пословица семь раз отмерь, один раз отрежь, начинает обретать некое подобие практичности. По пословице мы должны были провести семь разграничений. Восьмая граница уже не мера, а рез, поскольку отсекает и черную бесконечность диалектического монолита и белую. Но по рисунку разграничений не семь, а девять. Пословица ошибается? Девять раз отмерь один раз отрежь?
- -- Совпадение для продвинутых!!!! Красным цветом на рисунке обозначены границы между полями -3 и -4, а так же между полями -7 и - 8. Эти границы влияют на границы зеленого поля опосредованно, они полуфункциональны. Цифры не могут нам помочь найти аналогию понятную сознанию. Пора переходить к нотам. Если начать деление не с инертной границы -1v 1 а с известного полутона До v Ре. То зеленое поле превратится в скрипичный ключ, а вышеозначенные неполноценные границы в отсутствующие черные клавиши фортепиано.
- -- Пословица семь раз отмерь, один раз отрежь, начинает обретать некое подобие практичности. По пословице мы должны были провести семь разграничений. Восьмая граница уже не мера, а рез, поскольку отсекает и черную бесконечность диалектического монолита и белую. Но по рисунку разграничений не семь, а девять. Пословица ошибается? Девять раз отмерь один раз отрежь?