ПОЧЕМУ СЕГОДНЯ САМАЯ БОЛЬШАЯ ЛУНА?
Поступательное движение - есть движение, при котором, хотя бы одна прямая, перпендикулярная направлению движения и связанная с физическим телом, перемещается параллельно самой себе (определение заимствовано из теоретической механики).
Следовательно, как бы ни двигалось физическое тело в пространстве, его ось абсолютного вращения будет всегда оставаться параллельной самой себе.
Отсюда следует, что Земля движется вокруг Солнца поступательно и её ось суточного вращения всегда остается параллельной самой себе. Поэтому в периоды самого протяженного дня и самой короткой ночи на северном полушарии Земли ось суточного вращения Земли направлена вдоль линии соединяющей Солнце с Землею, а точнее проекция оси на плоскость эклиптики. В периоды весеннего и осеннего противостояния (день равноденствия) ось суточного вращения Земли будет перпендикулярна линии соединяющей Солнце и Землю, а точнее её проекция на плоскость эклиптики.
В объективной астрономии мною утверждалось, что Луна движется в плоскости экватора Земли, если не считать влияние притяжения Солнца на её движение. Притягивающая мощь Солнца оказывает влияние на её движение относительно Солнца в зависимости от её фактического положения относительно Земли и Солнца. Следовательно, в период весеннего или осеннего равноденствия полная Луна, наблюдаемая ночью, будет находиться ближе к поверхности Земли, так как на линии притяжения Луны Солнцем находится Земля. Если в эти периоды равноденствия наблюдается новолуние, то есть наблюдается полная Луна днем, то она будет находиться в самой удаленной точке от поверхности Земли.
"Надо бы влияние этих сил притяжения в процессе динамики движения рассмотреть. Картина может измениться вследствие сдвига фаз между силой и её влиянием на положение. Все же второго порядка уравнения интегрируются-то. Каждый порядок в представлении по Фурье может давать сдвиг до Пи пополам. Что не может не сказаться на результатах обратного преобразования. Впрочем, задача хорошо решается и аналитически "в лоб". В приближении неподвижного, вследствие его массивности, Солнца".
Луна постоянно уравновешена притягивающей энергией Земли и уравновешена постоянно изменяющейся притягивающей энергией Солнца, так как расстояние между Луной и Солнцем постоянно изменяется, вследствие движения Луны вокруг Земли. Космические объекты Солнце, Земля и Луна находятся в движении - динамике и уравновешены между собой - статике, если понимать термин "статика" как уравновешенность, а не состояние покоя.
С точки зрения материалистической диалектики мышления, термины: "Статика" и "Динамика" выражают противоположные определения.
Что касается двойных стандартов, то, перефразировав древнюю пословицу: "Бойтесь данайцев дары приносящих", можно сказать: "Бойтесь математиков дары приносящих". Эти дары рождены в Ватикане. Мозговой центр, которого сосредоточен в США. Глупыми или "умными дураками", управлять легче.
В частности в теоретической механике, этот термин вошел как учение: "условий равновесия материальных тел под действием сил". Математики выражают понятие этого термина как учение об условиях равновесия тел в геометрической и аналитической статике. В основу аналитической статики лежит принцип возможных перемещений, дающий общие условия равновесия любой механической системы. Геометрическая статика основывается на так называемых аксиомах статики, которые выражают свойства сил, действующих на материальное тело.
В теоретической механике установлены основные аксиомы статики:
При этом рассматриваются решения следующих двух типов задач:
Необходимые и достаточные условия равновесия упруго деформируемых тел, а также жидкостей и газов рассматриваются соответственно в упругости теории, гидростатике и аэростатике.
При этом Даль пишет: "Сила есть отвлеченное понятие общего свойства вещества, тел, ничего не объясняющее, а собирающее только все явления под одно общее понятие и название. Силы природы, силы жизненные, неведомая причина, коей мы приписываем все явления. Мертвая сила, неодушевленной природы; живые, растительной и животной природы.
Научитесь мыслить категориями "Качество" и "Количество". При этом, изучив "Пролог" и мою физику, Вы поймете, что формула F = mv; выражает врожденную силу материи, то есть первый закон Ньютона, в исправленной мною редакции, и названный впоследствии математиками "законом инерции". Второй закон Ньютона неверен, так как он противоречит его закону о центральной силе, а закон всемирного тяготения есть чисто математическая формула, приписанная Ньютону, как автору закона о центральной силе.
Обратите внимание. В 9 лет он потерял обоих родителей. Сироту устроили в Военную школу при бенедиктинском монастыре.
В 1789 году приезжает в Париж, чтобы представить работу: "О численном решении уравнений любой степени", но она затерялась во время революции.
Революция пришла раньше, чем он смог решить, кем ему стать - монахом, военным или математиком. Фурье возвращается в Осер и преподает в школе, в которой прежде учился. Он активно содействует новой власти, и Фурье пригласили в Нормальную школу, организованную Национальным Конвентом для подготовки преподавателей (1794г.). Вскоре школу закрыли, но он успел обратить на себя внимание видных учёных: Лагранжа, Лапласа и Монжа. 1
В 1796г. он доказывает теорему о числе действительных корней алгебраического уравнения, лежащих между данными пределами. Эта теорема получила название Теорема Фурье. В 1818г. исследует, независимо от Ж. Мурайле, вопрос об условиях применяемости, разработанного И. Ньютоном метода численного решения уравнений. В своей монографии: "Аналитическая теория тепла", даёт вывод уравнения теплопроводности в твёрдом теле, и разрабатывает методы интегрирования при различных граничных условиях. Метод Фурье состоял в представлении функций в виде тригонометрических рядов Фурье.
Работы И. Ньютона после его смерти к этому времени уже были переведены на французский язык при содействии Вольтера. Потом Фурье нашёл формулу представления функции с помощью интеграла, играющую важную роль в современной математике и доказал, что всякую произвольно начерченную линию, составленную из отрезков дуг разных кривых, можно представить единым аналитическим выражением.
В 1823г. независимо от Эрстеда открыл термоэлектрический эффект, при этом создал термоэлектрический элемент.
1 Именно они дали в 1807 году отрицательные отзывы на мемуары Фурье "Аналитическая теория тепла", которую он смог опубликовать, лишь став пожизненным секретарём Парижской академии в 1822 году.
Представление французского математика до крушения, и после крушения власти феодальной аристокра-тии и духовенства. После того как было создано масонское движение, все математики попали в сети этого движения как слепые котята. Но об этом читайте в приложении к этой статье. В приложении показана нелепость самого дифференцирования, а соответственно и интегрирования, которое со временем стали применять и к другим качественным свойства носителя.
Исходя из сказанного, приведу рисунок, объясняющий, почему Луна сегодня самая большая?
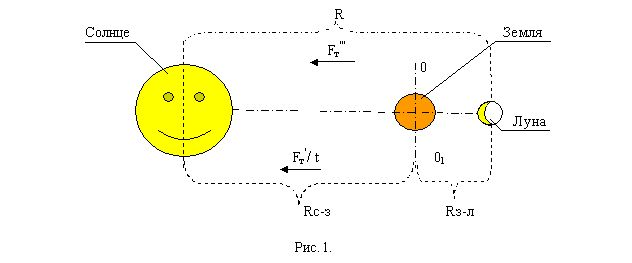
Притягивающая мощь Солнца или Мощь силы тяжести Земли по отношению к Солнцу равна: Fт'/ t = mз gс / (Rс-з)2;
Притягивающая мощь Земли или мощь силы тяжести Луны по отношению к Земле равна: Fт"/ t = mл gз / (Rз-л)2;
Притягивающая мощь Солнца или мощь силы тяжести Луны относительно Солнца, в тот момент времени, когда Луна находится за Землею на одной линии: Fт'"/ t = mл gс / R2;
При этом мы рассматриваем движение Земли относительно Солнца как идеальное физическое тело, то есть мы не рассматриваем её колебательное движение в направлении оси перпендикулярной её суточной оси и направлению движения Земли относительно Солнца.
В данной статье я не буду применять математические преобразования на базе элементарной математики. Считаю, что это будет излишним.
КАЗУИСТИКА* - ФУНДАМЕНТ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ.
* Казуистика (от латинского термина casus - случай). Теория абстрактно-логического применения к отдельным частным случаям общих догматических положений. В переносном значении - изворотливость в доказательствах ложных и сомнительных положений.
Вектор скорости и вектор направления внутри физического тела никогда не изменяют своего действия и всегда совпадают.
Это утверждение сделано на основании логичного анализа фундаментальных основ, которые изложены в теоретической механике на основе формальной логики мышления, а так же наблюдений в объективной реальности.
Математическая точка как свободное физическое, тело имеет шесть степеней свободы. В системе координат такая точка может двигаться, не только вдоль координатных осей, а и вращаться вокруг этих координатных осей.
Теоретическая механика раскладывает векторную скорость криволинейного движения на составляющие "радиальная" и "поперечная" и получает выражение
v = dr/dt = (dr/dt) в rR + (drо/dt) в r; (1) 2
При этом, опираясь на векторную алгебру: "Дифференцирование векторов по скалярному аргументу" получают уравнение:
![]() ; (1.1) 3
; (1.1) 3
2 Н.Н. Бухгольц Основной курс теоретической механики, Ч.1, изд-во "Наука", 1975г., стр.64.
3 Там же
Согласно законам элементарной алгебры, введение в одну часть уравнения (1.1) дополнительного единичного вектора "ро", нарушает равенство в этом уравнении, но теоретическая механика продолжает: "Скорость (какая?) как видно из этого выражения состоит из двух слагаемых. Первое из них [dr/dtвro] имеет тоже направление, что и радиус-вектор r, и характеризует изменение r по модулю".
Векторная алгебра там же (стр.41) говорит: "в общем случае в уравнениях 1. и 1.1. dr не равно dr. Равенство |dr| = dr имеет, очевидно, место лишь при dro/dt = 0 (второе слагаемое), при этом ro = const, то есть когда вектор r изменяется только по модулю". Следовательно, физическое тело как материальная точка движется равномерно и прямолинейно, то есть v = dr/dt, вектор направления ro = const. В случае криволинейного движения - утверждает теоретическая механика - вектор направления ro, имеет также то же направление, что и радиус-вектор r, при этом dr не равно dr.
Но радиус-вектор не может действовать сам по себе. Он действует в физическом теле как в материальной точке. Следовательно, в первом слагаемом вектор dr или как его называет теоретическая механика в этом слагаемом "модуль вектора" не изменил своего направления в физическом теле и совпадает с единичным вектором - вектором направления. Физическое тело продолжает движение в том же направлении относительно самого себя, то есть вы бежали прямо по улице и повернули в переулок. Как был вектор скорости вашего бега направлен перпендикулярно к вашей груди, так он и остался, ей перпендикулярен.
"Чтобы выяснить смысл второго слагаемого, - пишет далее теоретическая механика - заметим, что |dro| =
Направленный отрезок ОМ, показанный на рисунке (см. рис.33), выражает радиус-вектор r. В левой части уравнений (1. и 1.1.) этот радиус-вектор r представляет выражение: v = dr/dt, где символ r выражает расстояние, пройденное физическим телом как материальной точкой от длительности движения, то есть от времени t. Расстояние на этом рисунке показать не возможно. Следовательно, не радиус-вектор r, а расстояние, которое в физике обозначается символом "s". Это расстояние "s" не соответствует, указанному на рисунке радиус-вектору.
В объективной реальности не скорость движения является функцией пути от времени, а наоборот: "расстояние есть функция скорости от времени этого движения. Что от чего зависит? Изменение выражения вашего лица от изменения его отражения в зеркале или само отражение в зеркале зависит от изменения выражения вашего лица? Или в высшей математике и в математической физике, также как у Дориана Грея все изменения происходят на его портрете. Но портрет Дориана Грея это плод воображения писателя. Следовательно ...
Направленный отрезок ОМ - радиус-вектор r, который совместно с углом
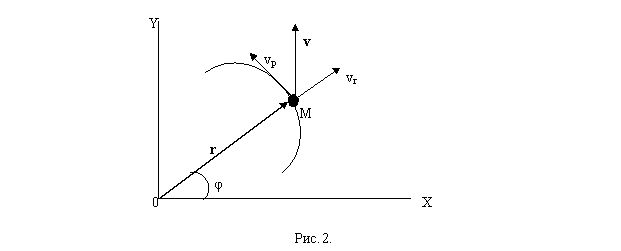
С другой стороны отрезок ОМ не как радиус-вектор выражает геометрическую сумму координат точки М в декартовых координатах. Но в декартовых координатах в плоской системе координат точка М может быть задана или её двумя проекциями на эти координатные оси или отрезком ОМ и величиной угла ме-жду какой-нибудь координатной осью, что не удобно при построении (см. Начертательную геометрию), но допустимо. Третьего не дано.
Задание координат точки М отрезком ОМ и углом
При этом отрезок ОМ никак не связан с направлением и величиной скорости движения точки М. Выше я приводил пример из технологии машиностроения о профилировании кулачка в одношпиндельном прутковом автомате при его технологической наладке на конкретную деталь.
При этом приводится рисунок (см. рис.3):

На рис. 3 показана геометрия стрелок. Точно также легко показать и аналогично доказать это не только на единичном векторе - орте, а и на самом векторе или его модуле. Геометрическая стрелка всегда останется стрелкой, как бы вы её не называли и какие символы бы ей не присваивали. Но главное здесь другое.
Выражение
Теоретическая механика пишет: "Положение тела в любой момент времени t определяется уравнением
Давайте будем рассуждать логично. Геометрическая стрелка "вектор" всегда останется стрелкой, которой можно присваивать любые названия и обозначения. Законы геометрии от этого не изменятся.
На рисунке мною показаны векторы как геометрические стрелки. При этом я избегаю процессов дифференцирования, так как "на превеликий жаль маю суттєвi прогалини в освiтi". Ибо еще в студенческие годы мой ум не воспринял высшую математику в части разделы "Дифференцирование" и "Интегрирование", так как они противоречили здравому смыслу и элементарной математике, которой я владел безукоризненно еще со школьной парты. Поэтому, привязываясь к теоретической механике, я буду стараться следовать ей.
При этом вы должны понимать, что вектор скорости V принадлежит физическому телу в положении "А" на какой-то одной точке траектории.
4 Н.Н. Бухгольц Основной курс теоретической механики, Ч.1, изд-во "Наука", 1975г., стр.40.
5 Там же, стр.96
На рисунке эти положения тела совмещены и показаны на одной точке траек-тории. Дорисуйте координатные оси и ваш радиус-вектор, выходящий из начала координат в точку 0 траектории будет выражать координату этой точки на траектории, но обязательно с углом его поворота. Но, для того чтобы рисунок был реальным необходимо второе положение A' физического тела на траекто-рии показать на другой точке 0' этой траектории. Вектор V' будет выходить из этой точки 0', а второй радиус-вектор будет соединен с этой точкой 0', которая на рисунке не показана.
На рисунке физическое тело параллелепипед (спичечный коробок) как материальная точка движется в направлении вектора V. Согласно уравнению 1 и векторной алгебре, вектор v (на рис.4 он обозначен символом V), который равен согласно уравнению 1. и 1.1. (dr/dt), но, в самом деле, выражает изменение расстояния по времени (ds/dt). В первом случае, когда первое слагаемое равно век-тору скорости [v = dr/dt], а единичный вектор rо в этом слагаемом равен const. При этом второе слагаемое равно нулю. Параллелепипед (спичечный коробок) будет двигаться прямолинейно и равномерно, что не соответствует изображению на рис.4. Траектория этого движения - прямая линия.
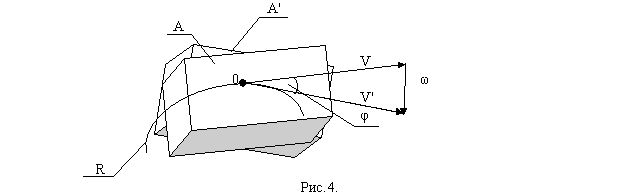
В том случае, когда второе слагаемое не равно нулю, а в первом слагаемом dr/dt, (на рис.4 его выражает вектор скорости V') не равен вектору скорости v = dr/dt (v = ds/dt) в уравнении 1. При этом второе слагаемое будет равно
Следовательно, параллелепипед (спичечный коробок) делает поворот с угловой скоростью
Геометрически радиус-вектор r связан с изменением вектора скорости. Но изменение радиус-вектора r зависит от изменения параметров движения точки как физического тела, а не наоборот как в примере с отражением лица в зеркале. Вызвано ли это изменение отражения гримасы лица зубной болью или субъект подобно обезьяне корчит эти гримасы перед зеркалом.
Рассмотрим этот процесс по элементам рис.5. Наше физическое тело "спичечный коробок" движется в первозданной Вселенной со скоростью V и врожденной силой F, согласно первому закону Ньютона, отредактированному, следовательно, наш "спичечный коробок" движется в единстве со скорость с энергией: W = FV,
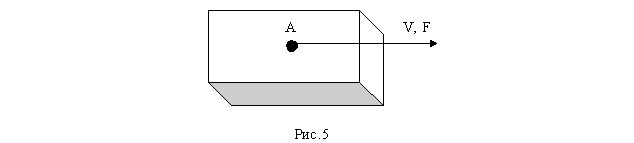
Спичечный коробок попадает под действие напряженности энергии от источника - ускоряющей величины центральной силы. У спичечного коробка возникает ускоряющая мощь, которая поворачивает его. На рисунке 6 изображен наш "спичечный коробок", попавший под действие "центральной силы" источника.
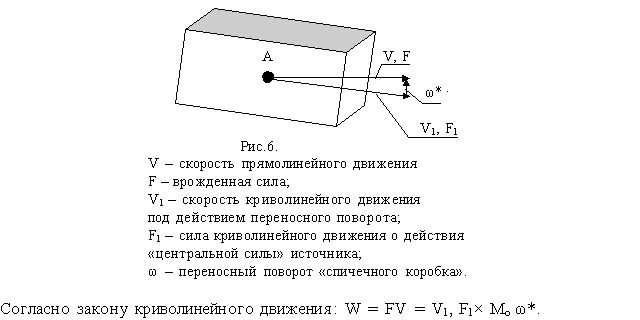
Переносный поворот осуществляется относительно оси, проходящей через точку А перпендикулярно плоскости рисунка.